Rappel Fonctions de référence
Soit f une fonction numérique définie par f(x)=ax² tel que a∈IR* et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→) est une parabole d'équation y=ax².

1) Si a>0 alors f est srictement croissante sur IR⁺=[0;+∞[ et srictement décroissante sur IR^-=]-∞;0].
f(0)=0 est le minimum de f sur IR.

2) Si a<0 alors f est srictement décroissante sur IR⁺ et srictement croissante sur IR^-.
f(0)=0 est le maximum de f sur IR.
3) La courbe (C) admet l'axe des ordonnées (Oy) comme axe de symétrie.

Exercice 1 tp

Soit f une fonction définie par f(x)=x² et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→). Construire la courbe (C).

Correction

On a D=IR. (C) est une parabole de sommet O.
On sélectionne quelques images des abscisses convenables pour connaitre l'allure de (C).

x	-2	-1	0	1/2	1	2	3
f(x)	4	1	0	1/4	1	4	9

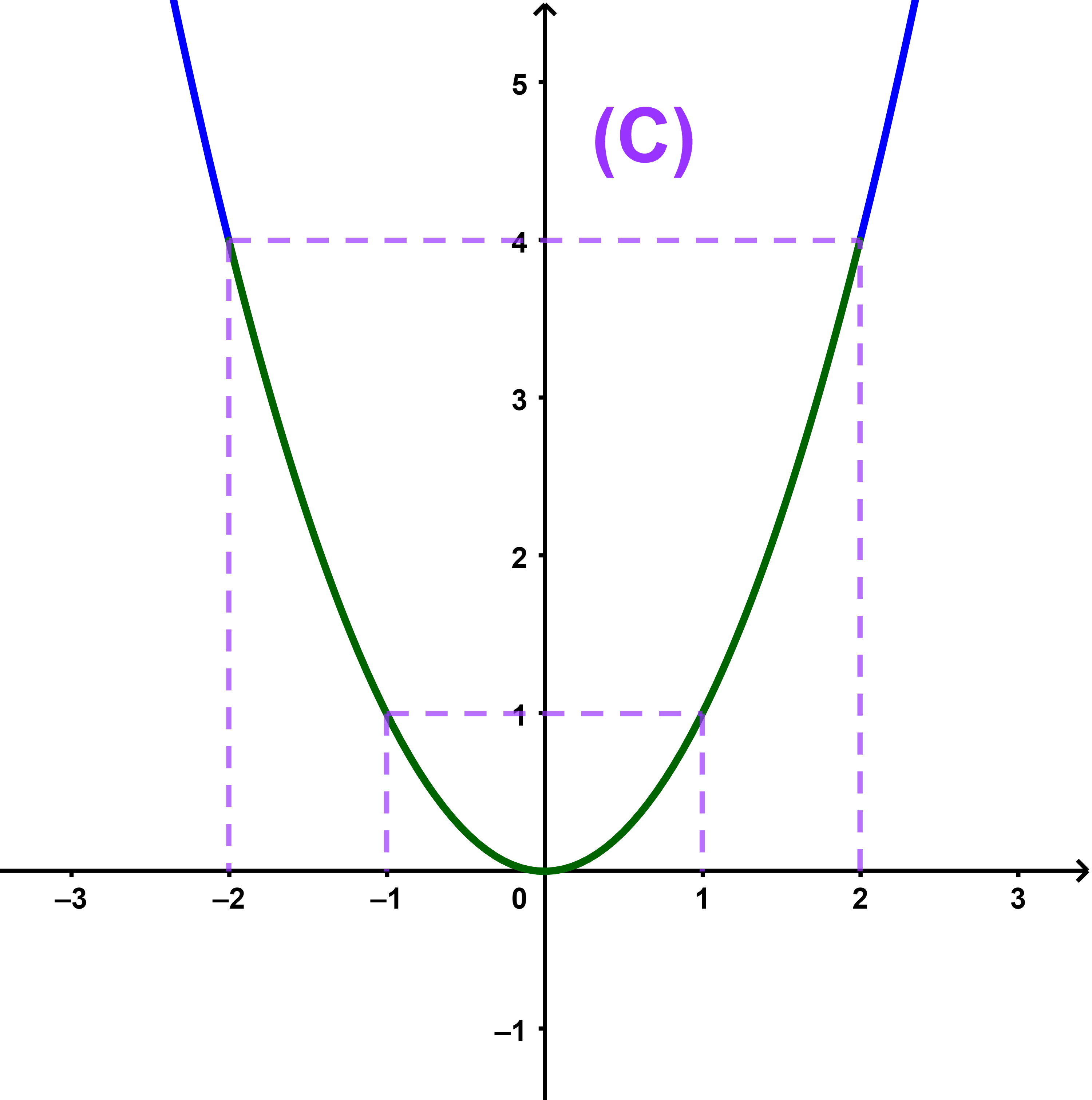
(a) (C) admet l'axe des ordonnées (Oy) comme axe de symétrie.
(b) Graphiquement f est strictement croissante sur IR⁺=[0;+∞[ et strictement décroissante sur IR^-=]-∞;0].
(c) f(0)=0 est la valeur minimale de f.

Tableau de variations

x	f	-∞		0		+∞
x	f		↘	0	↗

Exercice 2 tp

Soit f une fonction numérique définie par
f(x)=-2x² et (C) sa courbe dans un repère
orthonormé (O ; i^→ ; j^→). Construire (C).

Correction

On a D=IR. (C) est une parabole de sommet O.
On détermine quelques images convenables pour connaitre l'allure de la courbe de f.

x		-1	-1/2	0	1/2	1
f(x)		-2	-1/2	0	-1/2	-2

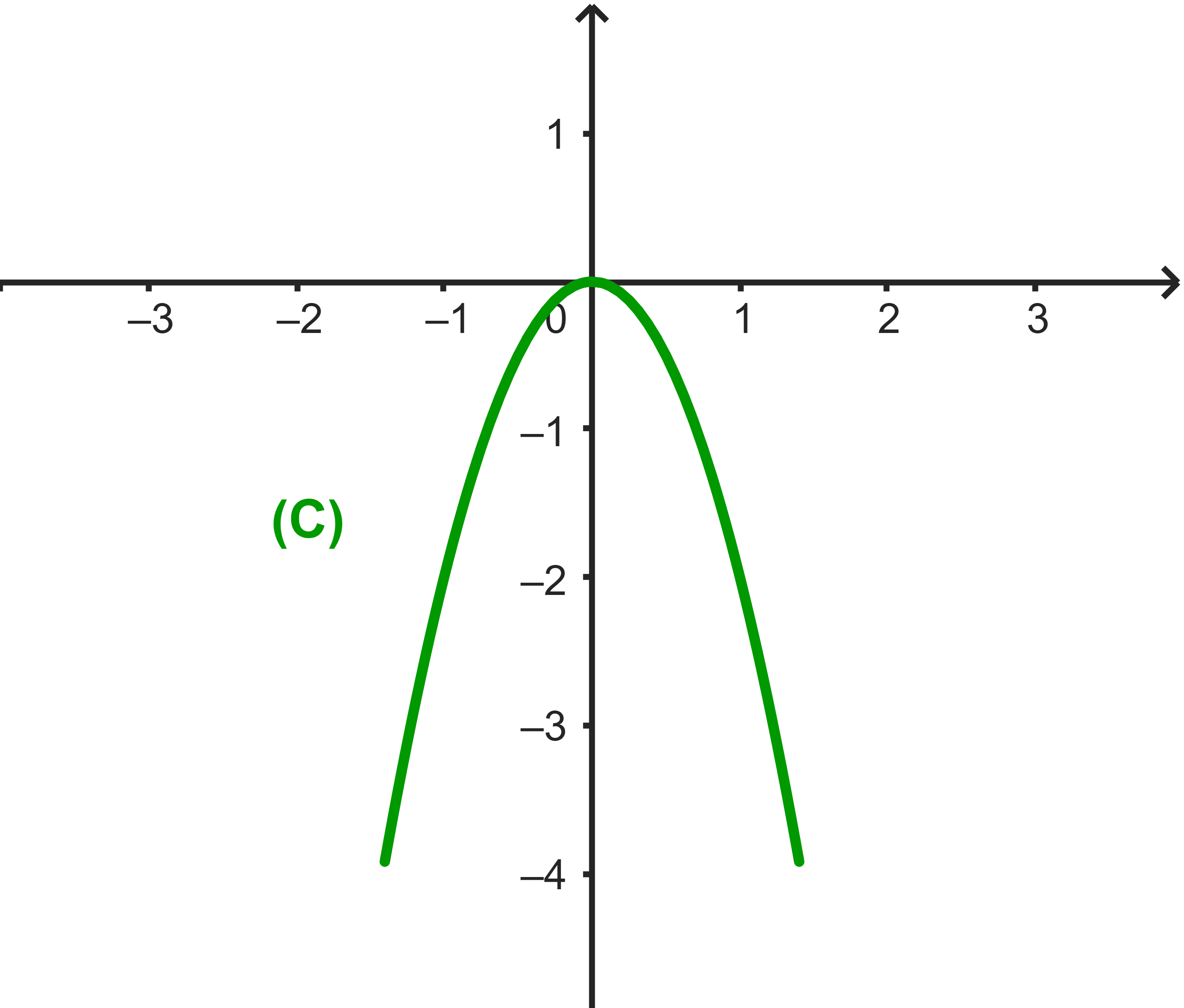
(a) La courbe (C) admet l'axe des ordonnées (Oy) comme axe de symétrie.
(b) Graphiquement f est strictement décroissante sur IR⁺=[0;+∞[ et strictement croissante sur IR^-=]-∞;0].
(c) f(0)=0 est la valeur maximale de f.

Tableau de variations

x		-∞		0		+∞
f			↗	0	↘