Rappel Fonctions de référence
Soit f une fonction définie par f(x)=ax²+bx+c tels que a;b;c∈IR (a≠0) et (C) sa courbe représentative dans un repère (O;i^→;j^→). (C) est une parabole de sommet

W(	-b	;f(	-b	))
	2a		2a

Exercice 1 tp

Soit f une fonction définie par
f(x)=2x²+1 et (C) sa courbe représentative dans un repère (O;i^→;j^→). Construire (C).

Correction

f est un polynôme donc D=IR=]-∞;+∞[.
1) Methode 1 déterminer les coordonées du centre W

-b	=	-0	= 0 et f(	-b	) = f(0) = 1
2a		-2.2		2a

(C) est donc une parabole de sommet W(0;1).

Notons qu'on peut construire la courbe sans utiliser la propriété. Il suffit de calculer des images de quelques abscisses convenables.

2) Méthode 2 remarquons que pour tout x de IR on a
2x²≥0 signifie 2x²+1≥1 signifie f(x)≥1
La courbe (C) est l'ensemble des points dont les ordonnées sont supérieurs ou égales à 1. La plus petite ordonnée est donc 1
et cela signifie que le point W(0;1) est en dessous de tous les points de la courbe.

x		-1	-1/2	0	1/2	1
f(x)		3	3/2	1	3/2	3

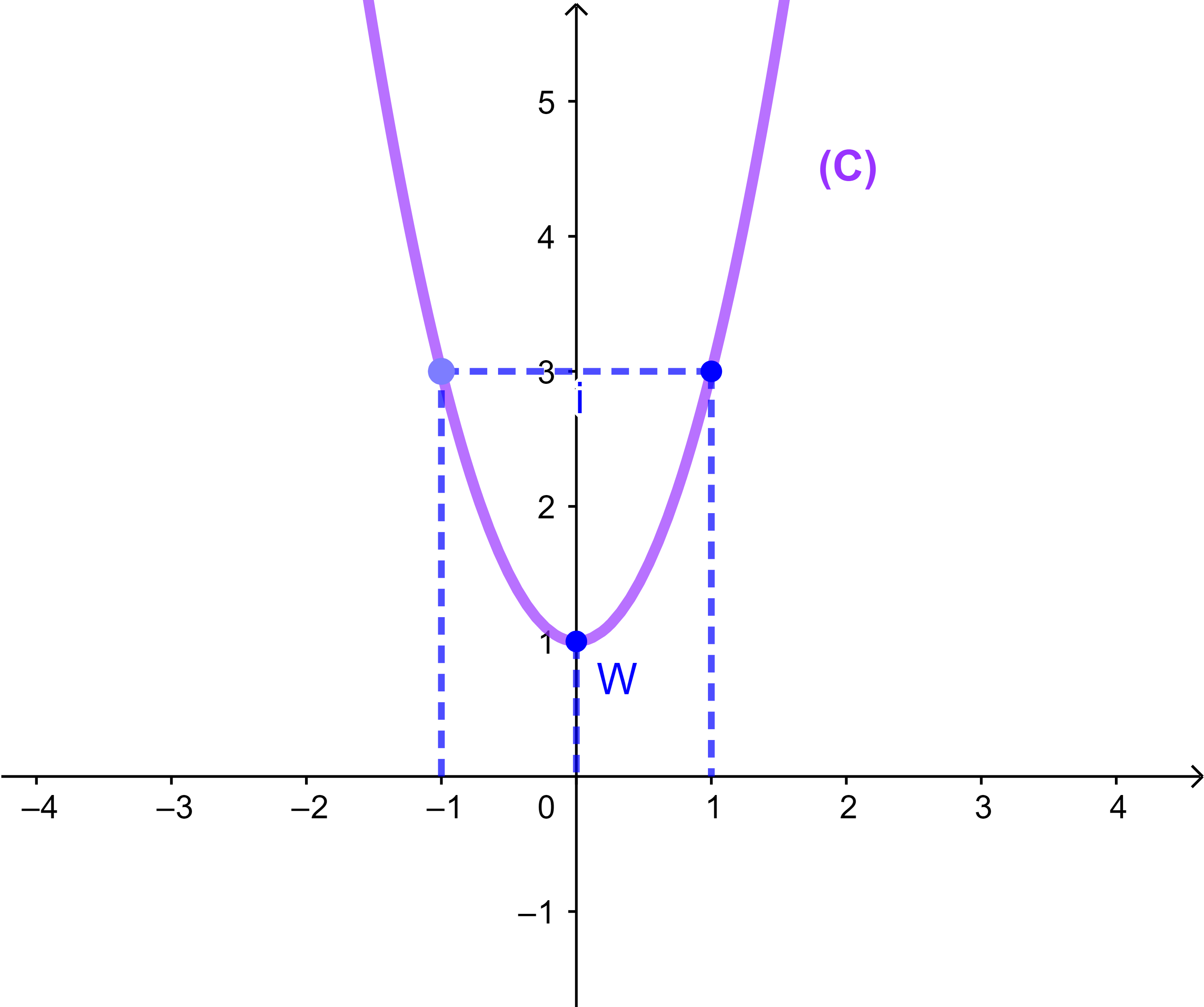
Tableau de variations

x		-∞		0		+∞
f			↘	1	↗

(a) La courbe (C) est une parabole de sommet I(0;1) et d'axe de symétrie d'équation x=0.
(b) f est strictement décroissante sur IR^- et strictement croissante sur IR⁺.
(c) f(0)=1 est la valeur minimale de f.