Exercice 1 tp

Soit f une fonction numérique définie par
f(x)=2x²-4x+1 et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Déterminer l'ensemble de définition D.
2) (a) Construire la courbe (C).
(b) Tracer le tableau de variations de f.
3) (i1) Résoudre graphiquement l'équation (E):f(x)=0.
(i2) Résoudre graphiquement l'inéquation (I):f(x)≤0.

Correction

1) f est un polynôme donc D=IR.
2) (a) La courbe (C).
f est un trinôme donc (C) est une parabole de sommet

w(	-b	;	f(	-b	))
	2a			2a

ainsi w(1;-1).
Nous choisissons des abscisses convenables de quelques points pour connaitre l'allure de la courbe

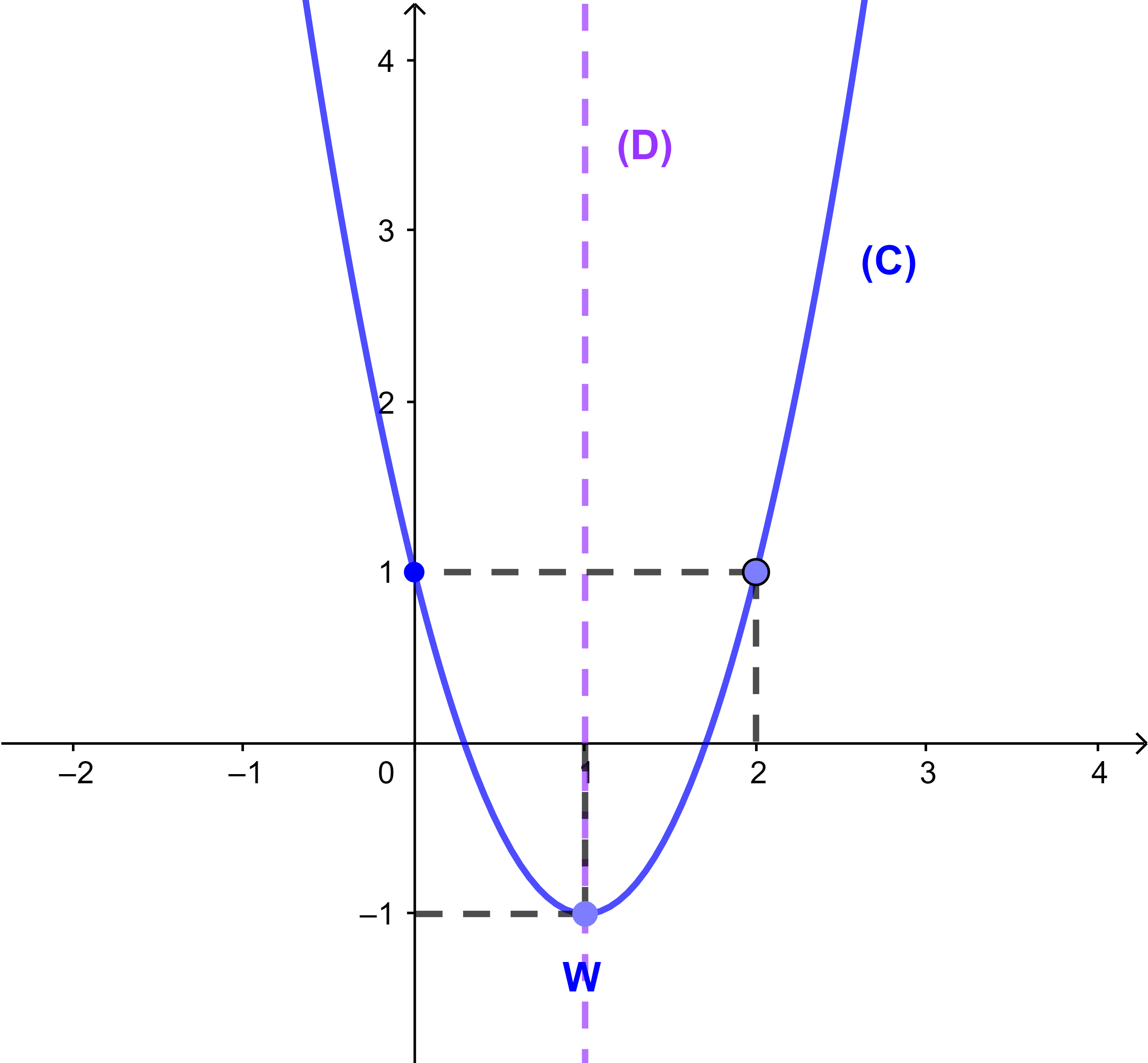
Alors f est strictement décroissante
sur ]-∞;1[ et strictement croissante sur ]1;+∞[.
(b) Tableau de variations

x		-∞		1		+∞
f			↘	-1	↗

(b) Résolutions de l'équation f(x)=0.
Le nombre de points de renconte de (C) avec l'axe des abscisses est 2 donc l'équation f(x)=0 admet deux solutions a et b
avec 0<a<1 et 1<b<2.

(c) Résolutions de l'inéquation f(x)≤0, Nous déterminons les intervalles ou (C) est au-dessous de l'axe des abscisses.
Dans l'intervalles [a;b] la courbe (C) est au dessous de (Ox)
donc l'ensemble des solutions de f(x)≤0
S=[a,b] tels que a et b sont les deux solutions de l'équation f(x)=0.