تذكير الدوال المرجعية.
الدالة المتخاطة f هي دالة معرفة كما يلي

f(x) =	ax+b
	cx+d

حيث a و b و c و d أعداد معلومة و c≠0 و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) (C) هذلول مركزه W

W(	-d	;	a	)
	c		c

2) (C) يقبل مقاربين

(D): x=	-d	و (D'): y=	a
	c		c

تمرين 1 tp

لتكن f دالة عددية معرفة بما يلي

f(x) =	-2x+1
	x-1

D={x∈IR /x-1≠0 }=]-∞;1[∪]1;+∞[
(C) هذلول مركزه W(1;-2).

المستقيمان (D):x=1 و (D'):y=-2 مقاربان للمنحنى (C).

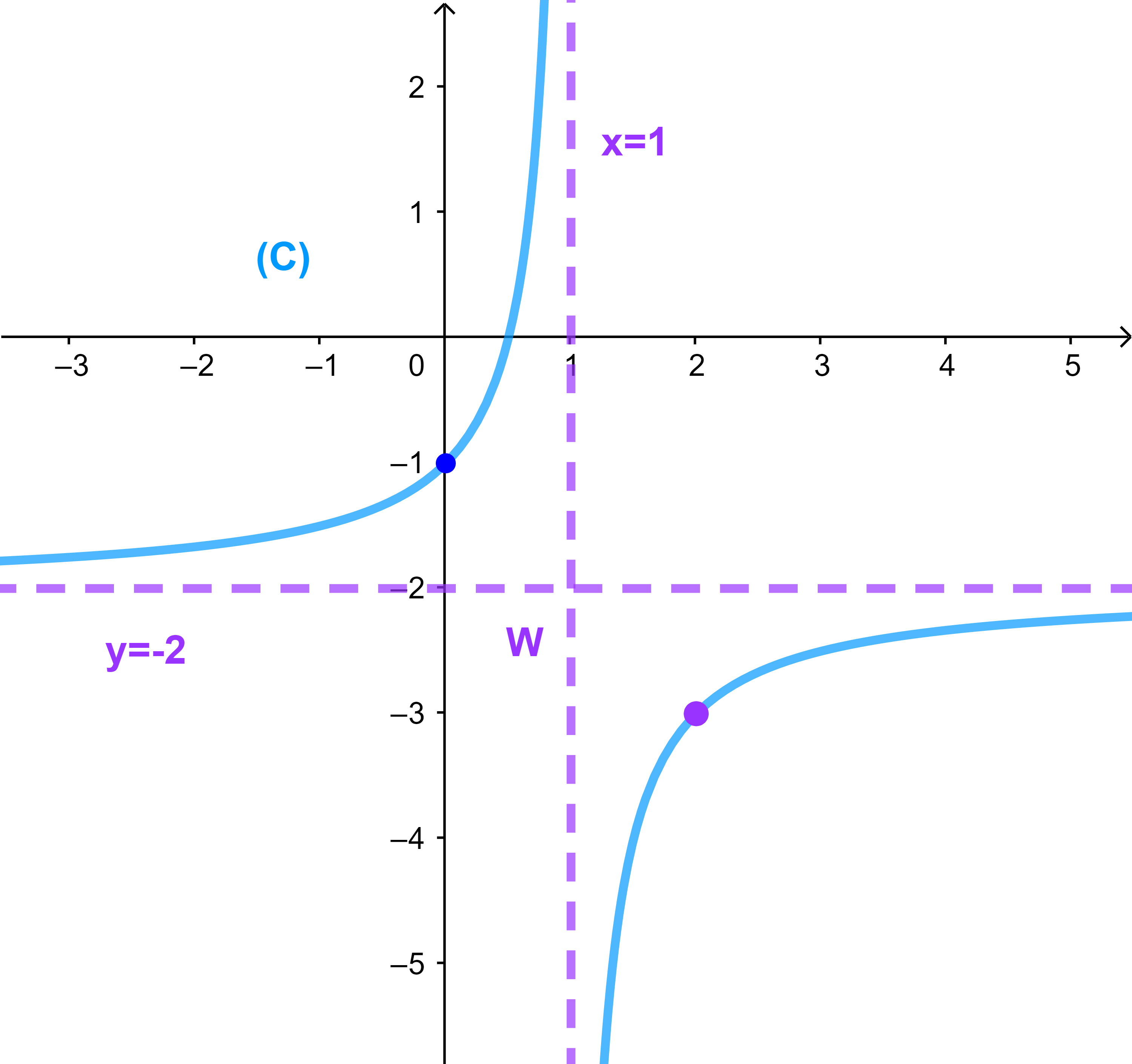
f تزايدية قطعا على ]1;+∞[
وتزايدية قطعا كذلك على ]-∞;1[.
جدول التغيرات

x		-∞		1		+∞
f			↗		↗

لاحظ أنه يمكن انشاء المنحنى دون استعمال الخاصية بتعيين صور أفاصيل مناسبة لبعض نقط المنحنى.

تمرين 2 tp

لتكن f دالة عددية معرفة كما يلي

f(x) =	-x+2
	x

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
حدد دالة g بحيث f(x)=g(x)-1 وأنشئ المنحنى (C).

تصحيح

f معرفة يعني x≠0 اذن D=IR*=]-∞;0[∪]0;+∞[.

ليكن x∈D.

f(x) =	-x	+	2	= -1 +	2
	x		x		x

نصع

g(x) =	2
	x

منحنى الدالة g هذلول مركزه O(0;0).
f(x)=g(x)+(-1) اذن لكل قيمة x نحدف 1 من صورتها بواسطة f.

(C) هذلول مركزه W(0;-1).
نعين صور أفاصيل مناسبة لبعض نقط المنحنى.

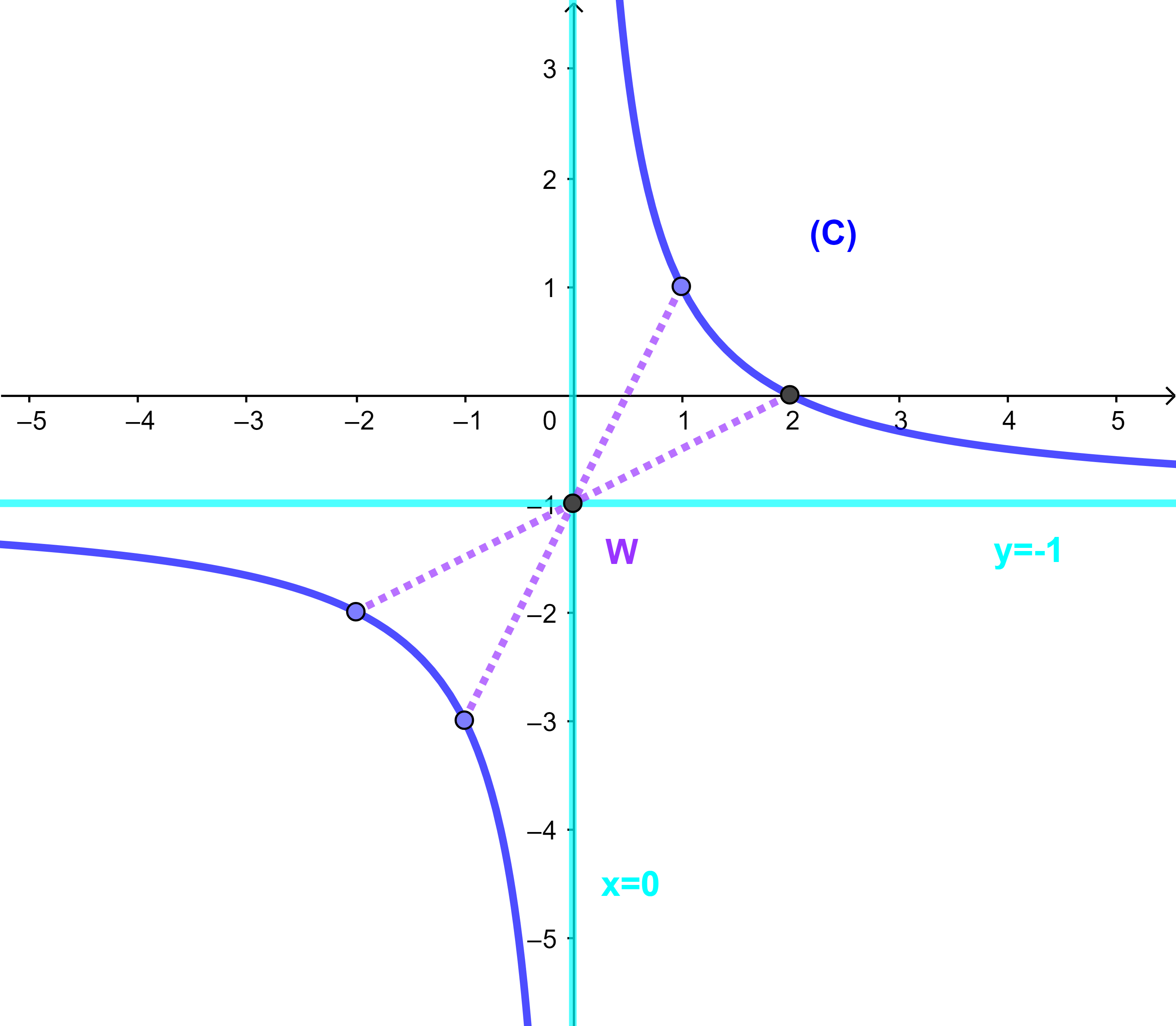
هندسيا f تناقصية قطعا على ]0;+∞[
وتناقصية قطعا كذلك على ]-∞;0[.

المستقيمان (D): x=0 و (D'): y=-1 مقاربان للمنحنى (C).

جدول التغيرات

x		-∞		0		+∞
f			↘		↘