عموميات حول الدوال العددية (7)
2.2 الدالة الزوجية
2.2.1 انشطة
لتكن f دالة عددية لمتغير حقيقي x بحيث
f(x)=x².
1) حدد Df مجموعة تعريف f.
2) تحقق ان Df مجموعة ممركزة.
3) قارن f(x) و f(-x) حيث x∈Df.
تصحيح
1) f دالة حدودية اذن Df=IR.
2) المجموعة IR
ممركزة عند الصفز
اذن لكل x∈IR لدينا -x∈IR اذن Df مجموعة ممركزة.
3) نقارن بعد ذلك f(x) و f(-x)
ليكن x∈IR لدينا f(-x)=(-x)²=x²
ومنه فان
f(-x)=f(x)
نقول اذن ان الدالة f دالة زوجية.
2.2.2 تعريف
لتكن f دالة عددية لمتغير حقيقي x
و D مجموعة تعريفها
نقول ان f دالة زوجية
اذا تحقق ما يلي
1) لكل x∈D فان -x∈D.
2) لكل x∈D فان f(-x)=f(x).
2.2.3 التأويل الهندسي
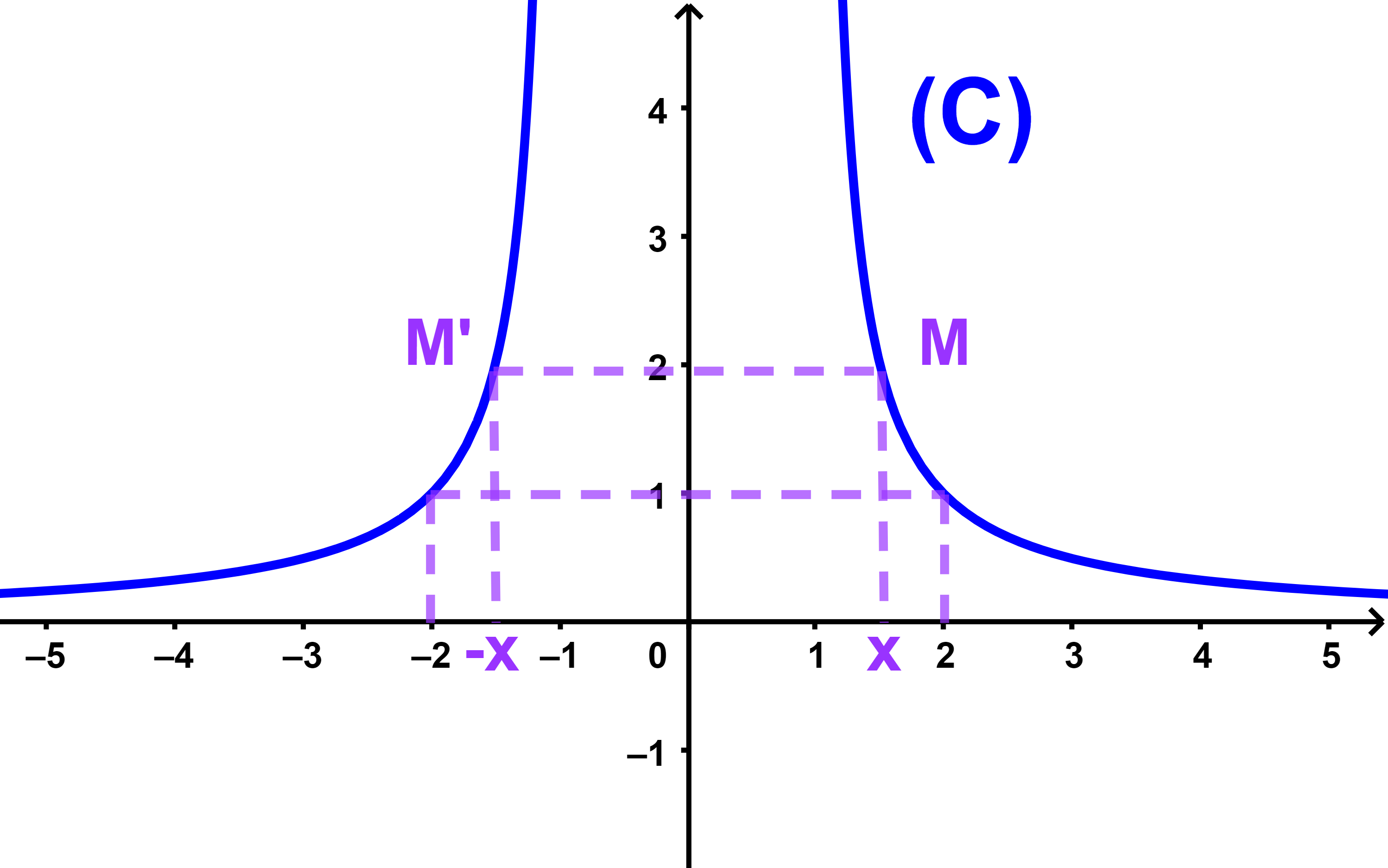
لتكن f دالة زوجية و Cf منحناها الممثل في المعلم (O;i→;j→).
بما ان f(-x)=f(x) حيث x∈IR
فان النقطتين M(x;f(x)) و M'(-x;f(x))
مماثلثان بالنسبة لمحور الأراتيب.
2.2.4 خاصية
منحنى دالة زوجية مماثل بالنسبة لمحور الأراتيب
تمرين 1 tp
لتكن f دالة عددية لمتغير حقيقي x ومعرفة كما يلي
| f(x) = | 1 |
| x² - 2 |
1) حدد مجموعة تعريف الدالة f
2) بين ان الدالة f زوجية
تصحيح
1) f معرفة اذا كان مقامها غير منعدم اي x²-2≠0
x²-2=0 يعني x²=2
يعني (x=√2 او x=-√2)
ومنه فان D=IR\{-√2;√2}.
2) نبين ان f دالة زوجية.
IR مجموعة ممركزة
وبما ان -√2 و √2 لا ينتميان معا الى D فان D مماثلة بالنسبة للصفر
اذن لكل x∈D فان (-x)∈D.
ليكن x∈D.
نحسب
f(-x)
نعوض
x ب -x.
| f(-x) = | 1 |
| (-x)² - 2 | |
| = | 1 |
| x² - 2 |
اذن f(-x)=f(x) وبالتالي الدالة f زوجية.