عموميات حول الدوال (6)
تمرين 1 tp
لتكن f و g دالتين عدديتين معرفتين كما يلي
f(x)=tan²(x)
و
| g(x) = ( | 1 | -1)( | 1 | +1) |
| cos(x) | cos(x) |
1) حدد مجموعة تعريف كل من f و g.
2) قارن بين f و g.
تمرين 2 tp
لتكن f دالة عددية معرفة كما يلي
f(x)=√(x²-3).
1) احسب صورة كل من الاعداد التالية
-3 و -1 و 0 و 2 بواسطة الدالة f.
2) حد من بين الأعداد التالية -1 و 0 و √(2) التي لها صورة بالدالة f.
3) حدد مجموعة تعريف الدالة f.
تمرين 3 tp
نعتبر الدالة العددية f المعرفة كالتالي
| f(x) = | 1 |
| x²-2 |
1) حدد مجموعة تعريف الدالة f.
2) بين ان الدالة f زوجية.
تمرين 4 tp
لتكن f دالة معرفة على [-3;2] بجدول تغيراتها بحيث f(1)=0
| x | -3 | -1 | 0 | 2 | |||
| f | 1 | ↘ |
0 |
↗ |
3 | ↘ |
-2 |
1) انشئ منحنى يمكن ان يمثل الدالة f.
2) استنتج حلول في I كل من المتراجحات التالية
(a): f(x)≥0
(b): f(x)<0
(c): f(x)≥3.
تمرين 5 tp
لتكن f دالة عددية معرفة مبيانيا على المجال [a;b].
1) حدد صورة بالدالة f كل من
-2 و -1 و 1
وحدد سوابق العدد 0.
2) حل مبيانيا كل من المعادلات التالية
(e1): f(x)=0
(e2): f(x)=3
(e3): f(x)=-2
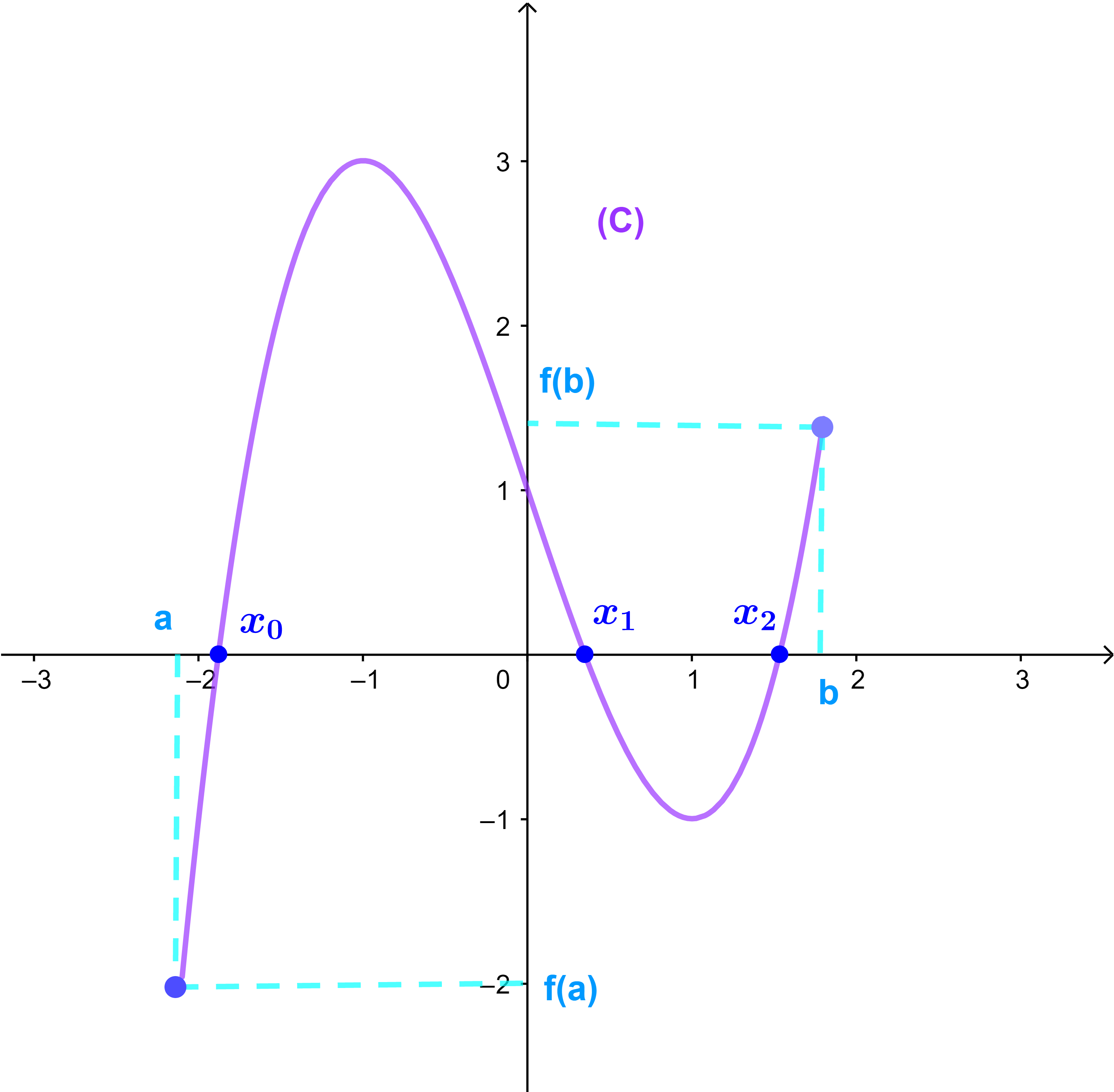
3) أطر حلول كل من المعادلات التالية
(e1): f(x)=1
(e2): f(x)=2
4) حل مبيانيا كل من المتراجحات التالية
(i1): f(x)≥0
(i2): f(x)≶3
(i3): f(x)≤-1
5) حدد تغيرات الدالة f على [a;b] وانشئ جدول تغيراتها..