Généralités sur les fonctions (6)
Exercice 1 tp
Soient f et g deux fonctions numériques définies par
f(x)=tan²(x)
et
| g(x) = ( | 1 | -1)( | 1 | +1) |
| cos(x) | cos(x) |
1) Déterminer le domaine de définition de chacune de f et g.
2) Comparer f et g.
Exercice 2 tp
Soit f une fonction numérique définie par
f(x)= √(x²-3)
1) Calculer l'image de chacun des éléments suivants
-3 ; -1 ; 0 et 2 par f.
2) Déterminer parmi les nombres -1 ; 0 et √(2) qui ont une image par f.
3) Déterminer le domaine de définition de f.
Exercice 3 tp
Soit f une fonction numérique définie par
| f(x) = | 1 |
| x²-2 |
1) Déterminer le domaine de définition de f.
2) Etudier la parité de la fonction f.
Exercice 4 tp
Soit f une fonction définie sur [-3;2] tel que f(1)=0 et le tableau suivant son tableau de variations.
| x | -3 | -1 | 0 | 2 | |||
| f | 1 | ↘ |
0 |
↗ |
3 | ↘ |
-2 |
1) Construire une courbe pouvant représenter la fonction f.
2) Déduire les solutions sur I de chacune des inéquations suivantes
(i1): f(x)≥0.
(i2): f(x)<0.
(i3): f(x)≥3.
Exercice 5 tp
Soit f une fonction définie graphiquement sur l'intervalle [a;b].
1) Donner les images par f de -2 ; -1 ; 1
et donner les antécédents de 0.
2) Résoudre graphiquement les équations suivantes:
(e1): f(x)=0.
(e2); f(x)=3.
(e3): f(x)=-2.
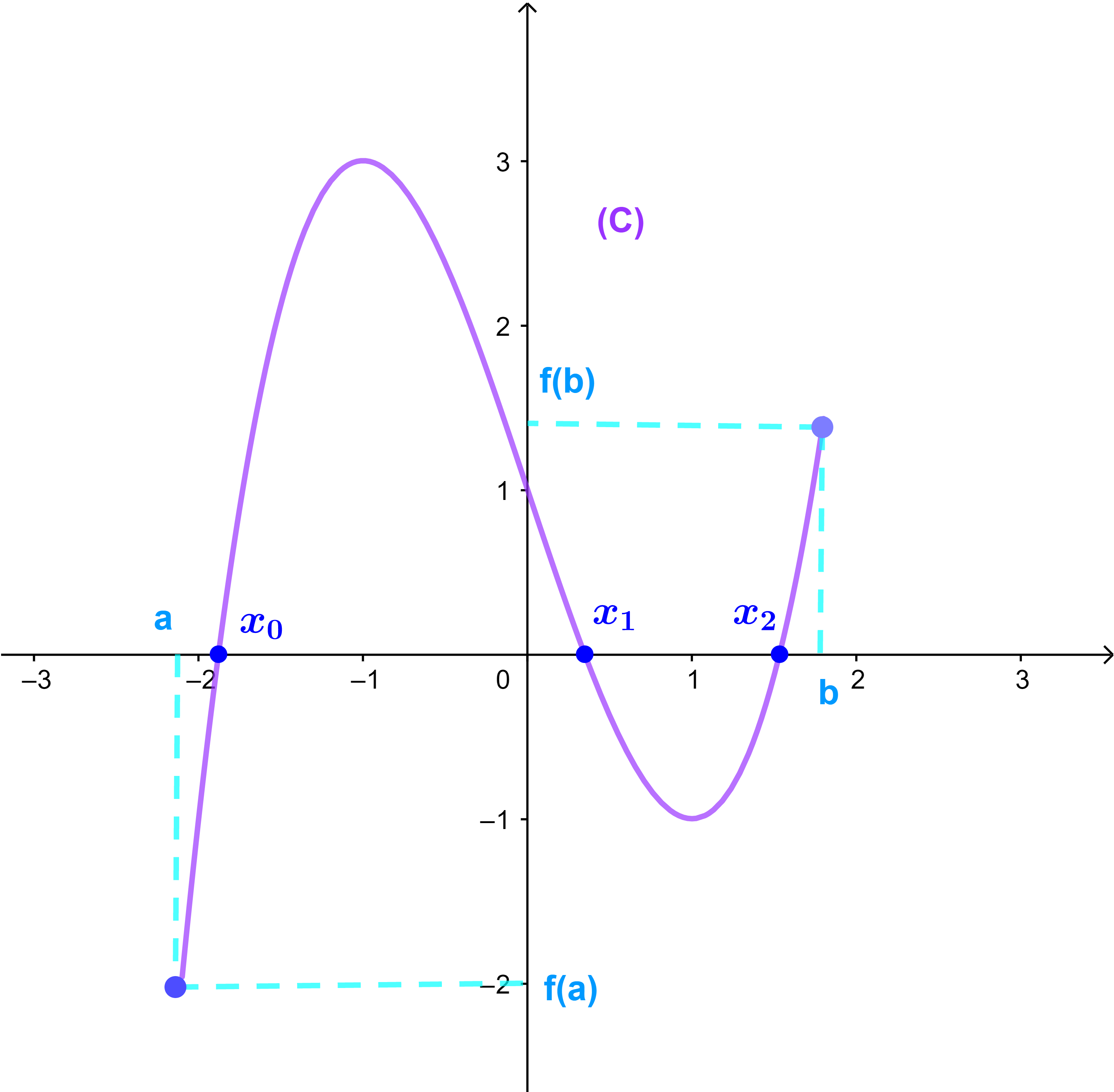
3) Donner des encadrements des solutions de chacune des équations suivantes
(e1): f(x)=1.
(e2): f(x)=2.
4) Résoudre graphiquement chacune des inéquations suivantes:
(i1): f(x)≥0.
(i2): f(x)≶3.
(i3): f(x)≤-1.
5) Déterminer les variations de f sur [a;b] et tracer son tableau de variations.