2- Opérations sur les vecteurs

2.1 Propriétés

Soient u^→ , v^→ et w^→ trois vecteurs.
Soient k et t deux réels.
1) Commutativité: u^→+v^→=v^→+u^→.
2) Associativité: (u^→+v^→)+w^→=u^→+(v^→+w^→).
3) Distributivité: k(u^→+v^→)=ku^→+kv^→.
4) k(tu^→)=ktu^→ et 1.u^→=u^→.
5) tu^→=0 signifie t=0 ou u^→=O^→.

Exercice 1 tp

Soient u^→ et v^→ deux vecteurs.
Simplifier
1) 2u^→-4(5u^→3v^→).
2) u^→-5v^→=7u^→-3v^→.

Exercice 2 tp

Soit u^→ un vecteur non nul.
Déterminer x tel que
8xu^→-3v^→=5(xu^→-v^→)+2v^→.

Exercice 3 tp

Soit EFGH un parallèlogramme.
Montrer que
1) EF^→+EH^→ =EG^→.
2) EF^→+EH^→ =EG^→.

Exercice 4 tp

Soient A et B deux points.
Tracer E et F tels que

AE→=	5	AB→
	3
AF→=	- 3	AB→
	2

Correction

On applique la propriété (3)

AE→=	5	AB→ = 5(	1	AB→)
	3		3

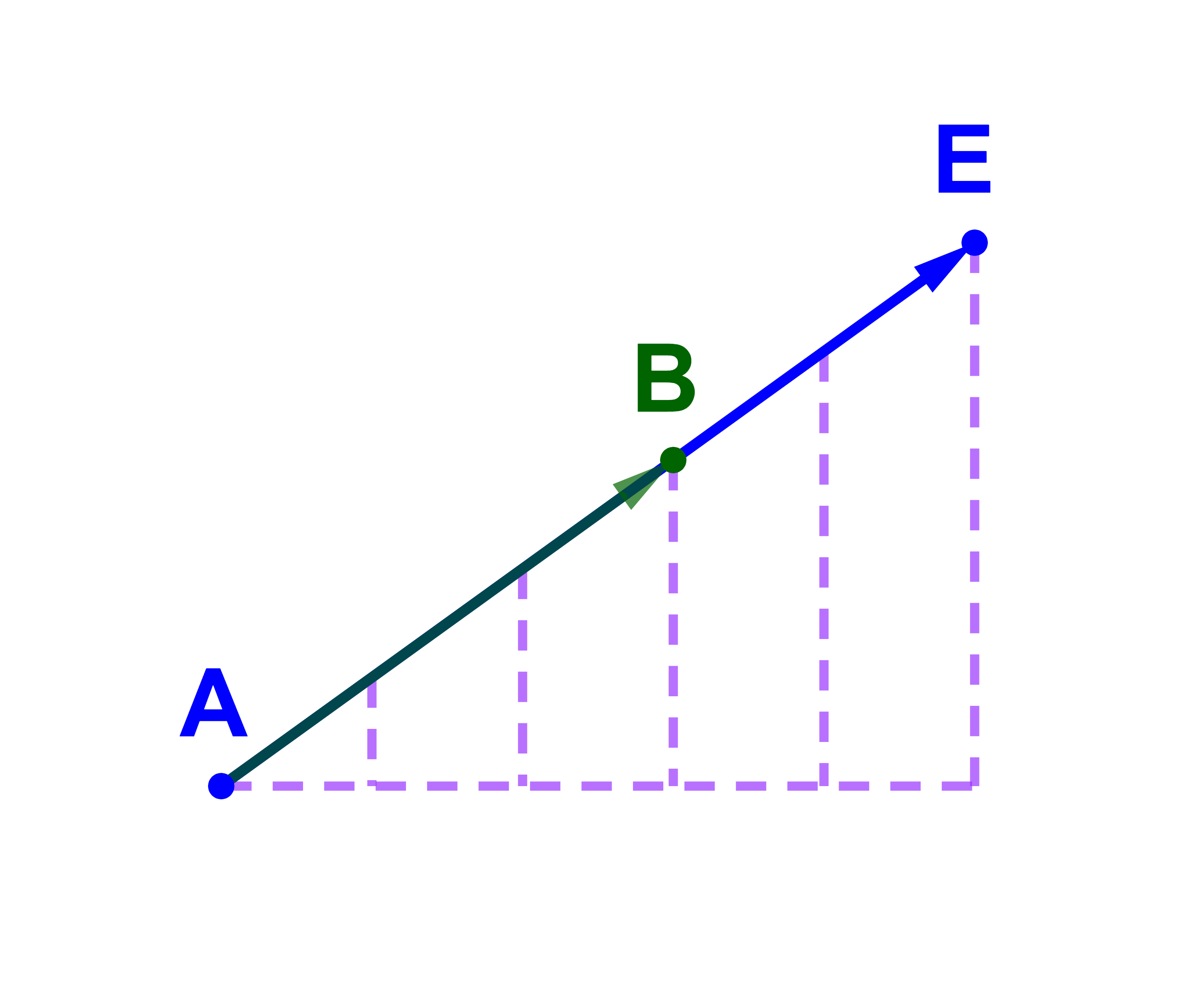
On dit que AE^→ et AB^→ sont colinéaires et donc les points A , B et E sont alignés.

AF→=	-3	AB→ = -3(	1	AB→)
	2		2

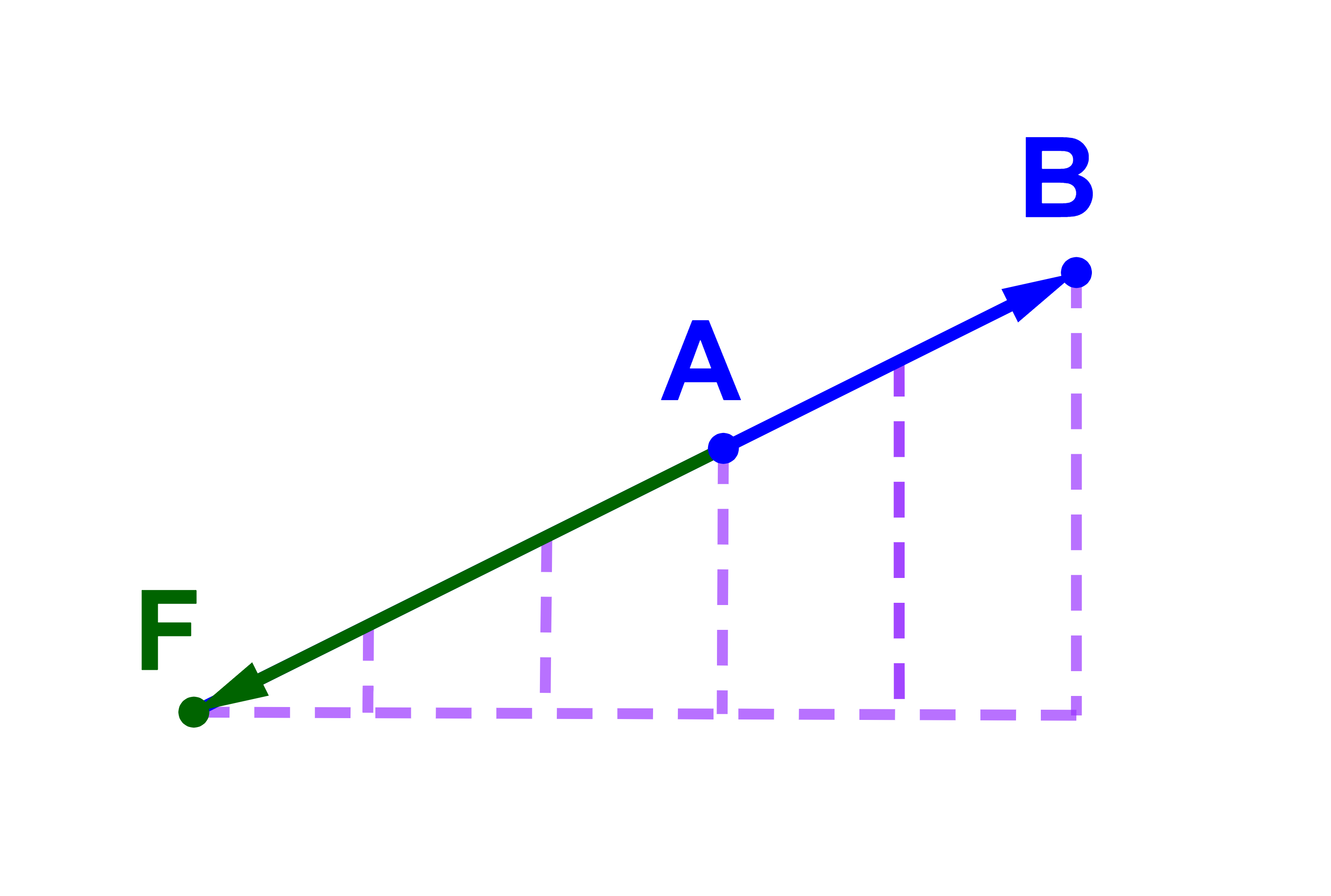
On dit que AF^→ et AB^→ sont colinéaires et donc les points A , B et F sont alignés.