الجداء السلي في المستوى (3)
تمرين 1 tp
لتكن u→ و v→ متجهتين.
اذا كان ||u→||=2 و
||v→||=4 و u→.v→= -0,5
احسب u→.(3u→-v→) و ||u→+v→||.
تمرين 2 tp
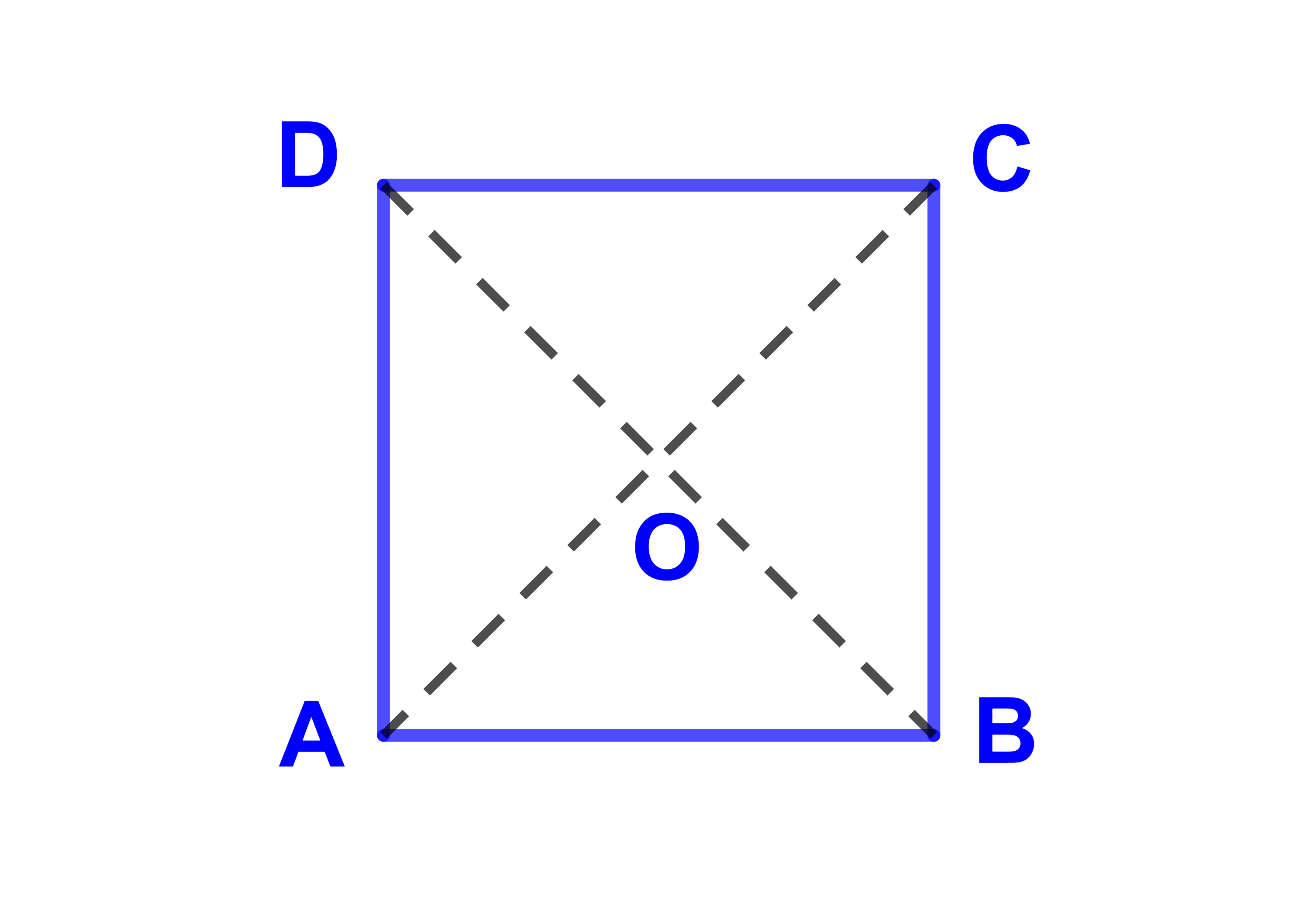
ليكن ABCD مربعا O وطول ضلعه 4. احسب
| AB→.AD→ | BC→.BO→ | |
| OD→.OC→ |
تصحيح
1) لدينا AB→⊥AD→ اذن AB→.AD→=0.
2) ABCD مربع اذن 2BO→=BD→ وبالتالي
| BC→.BO→=BC→. | 1 | BD→ |
| 2 |
| = | 1 | BC→.BD→ |
| 2 |
C هي المسقط العمودي للنقطة D على المستقيم (BC).
| BC→.BO→ = | 1 | BCxBC = 8 |
| 2 |
وبالتالي BC→.BO→=8.
3) لدينا OC→=OB→+BC→
اذن
OD→.OC→=OD→.(OB→+BC→)
=OD→.OB→
+OD→.BC→
لدينا OD→
=BO→
اذن OD→.OC→=-OB²+8.
بما أن OAB مثلث متساوي الساقين وقائم في O
فان 2OB²=AB² أي
| OB = | √2 | AB = 2√2 |
| 2 |
ومنه فان OD→.OC→=-8+8=0 وبالتالي OD→⊥OC→.