2- تطبيقات الجداء السلمي

2.1 العلاقات المترية في مثلث قائم

2.1.1 خاصيات

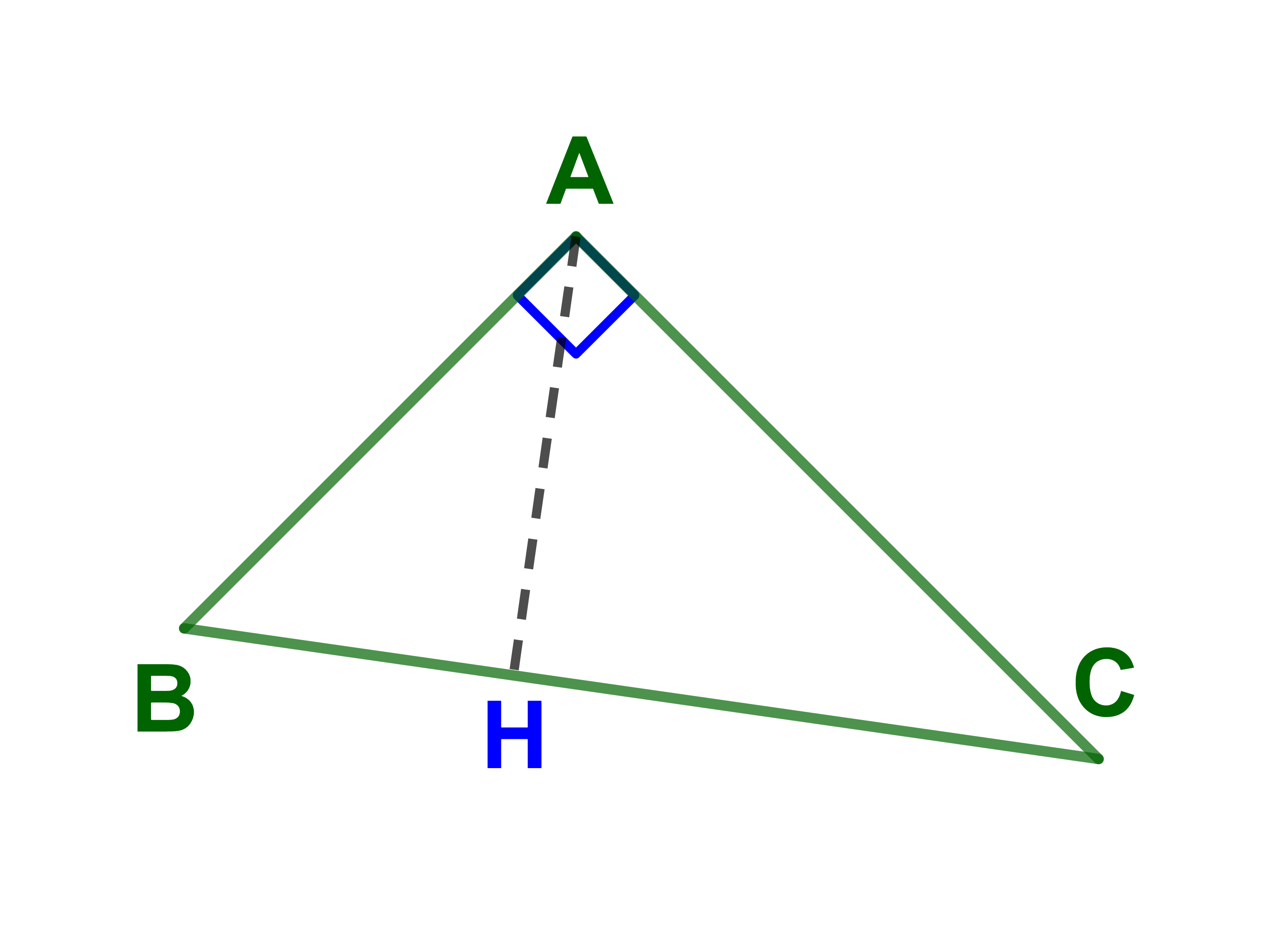
ليكن ABC مثلثا قائما في A و H المسقط العمودي للنقطة A على المستقيم (BC).

1) علاقة فيتاغورس
AB²+AC²=BC².
2) علاقات الأضلاع
CA²=CH×CB و BA²=BH×BC.

3) علاقة الارتفاع
AH²=HB×HC.

برهان
1) علاقة فيتاغورس
BC²=(AC^→-AB^→)² =AB²-2AB^→.AC^→+AC²
(AB)⊥(AC) اذن AB²+AC²=BC².
2) علاقات الاضلاع
لدينا BA²=BA^→.BC^→
بما أن H هي المسقط العمودي للنقطة A على (BC)
فان BC^→.BA^→=BH×BC.
وبالتالي BA²=BH×BC.
بنفس الطريقة نحصل على
CA²=CA^→.CB^→=CH×CB.

3) علاقة الارتفاع
HB^→.HC^→ =(AB^→-AH^→).(AC^→-AH^→)
=0-AH²-AH²-0+AH²=-AH²=-HB×HC.

تمرين 1 tp

ليكن BAC مثلثا قائما في B والنقطة H هي المسقط العمودي للنقطة B على (AC).
نعتبر BA=4 و AC=8.
1) احسب AH و HC و BH و BC و Â و Ĉ.
2) احسب مساحة المثلث BAC.