3.1.3 القيمة الوسطية

1) ميزة متقطعة لسلسلة احصائية

تعريف
أصغر قيم الميزة التي حصيصها المتراكم أكبر من أو يساوي نصف الحصيص الاجمالي تسمى قيمة وسطية للمتسلسلة الاحصائية.

مثال
نعتبر متسلسلة احصائية معرفة بالجدول الاحصائي التالي

قيم الميزة xi		1	2	3	4	5
الحصيص ni		5	15	10	7	13
الحصيص المتراكم Ni		5	20	30	37	50

الحصيص الاجمالي N=50 اذن N÷2=25

قيمة الميزة 2 حصيصها المتراكم هو 20 لكن 20 أصغر من 25
قيمة الميز 3 حصيصها المتراكم هو 30 وبما ان 30 أكبر من أو يساوي 25 فان 3 هي اصغر قيم الميزة التي حصيصها المتراكم أكبر من أو يساوي نصف الحصيص الاجمالي وبالتالي 3 هي القيمة الوسطية.

2) الميزة الاحصائية المتصلة أي المعرفة على مجالات.

مثال
نعتبر سلسلة احصائية معرفة بالجدول الاحصائي التالي

Ii		[1;5[	[5;9[	[9;13[	[13;17[	[17;21[
ni		50	70	50	120	110
Ni		50	120	170	290	400

نرمز ب M للقيمة الوسطية للسلسلة الاحصائية.
القية M هي أفصول النقطة H التي أرتوبها N÷2=200.

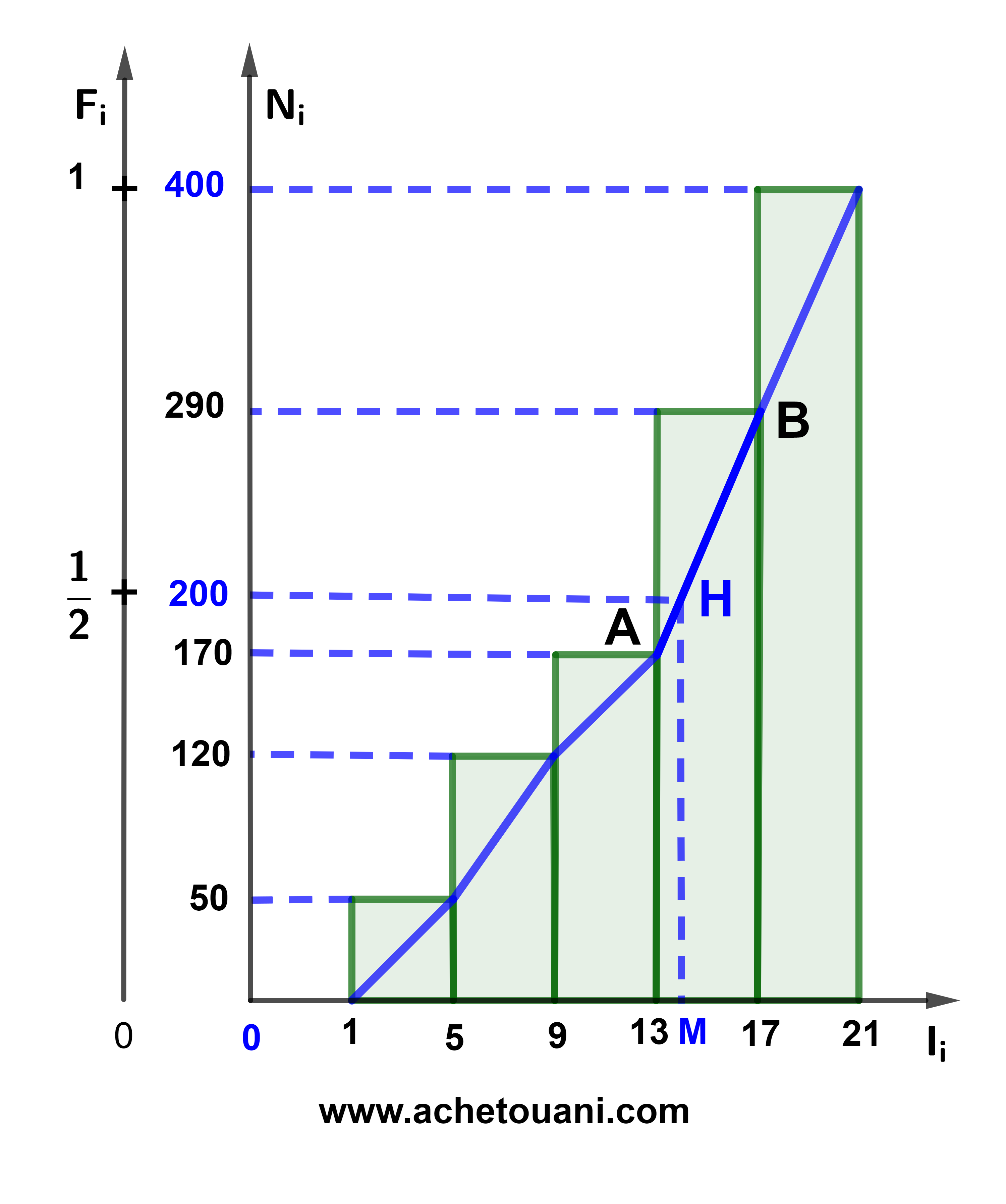
H(M;200)∈(AB) بحيث A(13;170) و B(17;290) يعني

M-13	=	200-170
17-13		290-170
M-13	=	30
4		120
M =	13 +	120
		120

القية الوسطية اذن M=14.