Transformations dans le plan (2)
1.3 Images par une symétrie centrale
1.3.1 Propriétés
Soit T=SO une symétrie centrale.
1) L'image d'un segment [AB] par T est un segment [A'B'] tels que A'=T(A) et B'=T(B).
2) (a) L'image d'une droite (D) par T est une droite (D') et de plus (D)||(D').
(b) L'image d'une demi droite D[AM) par T est une demi droite D[A'M') tels que A'=T(A) et M'=T(M).
3) L'image d'un cercle (C) de rayon R et de centre W par T est un cercle (C') de centre W'=T(W) et de même rayon R.
4) L'image d'un angle  par T est un angle Â' et ils sont de même mesure.
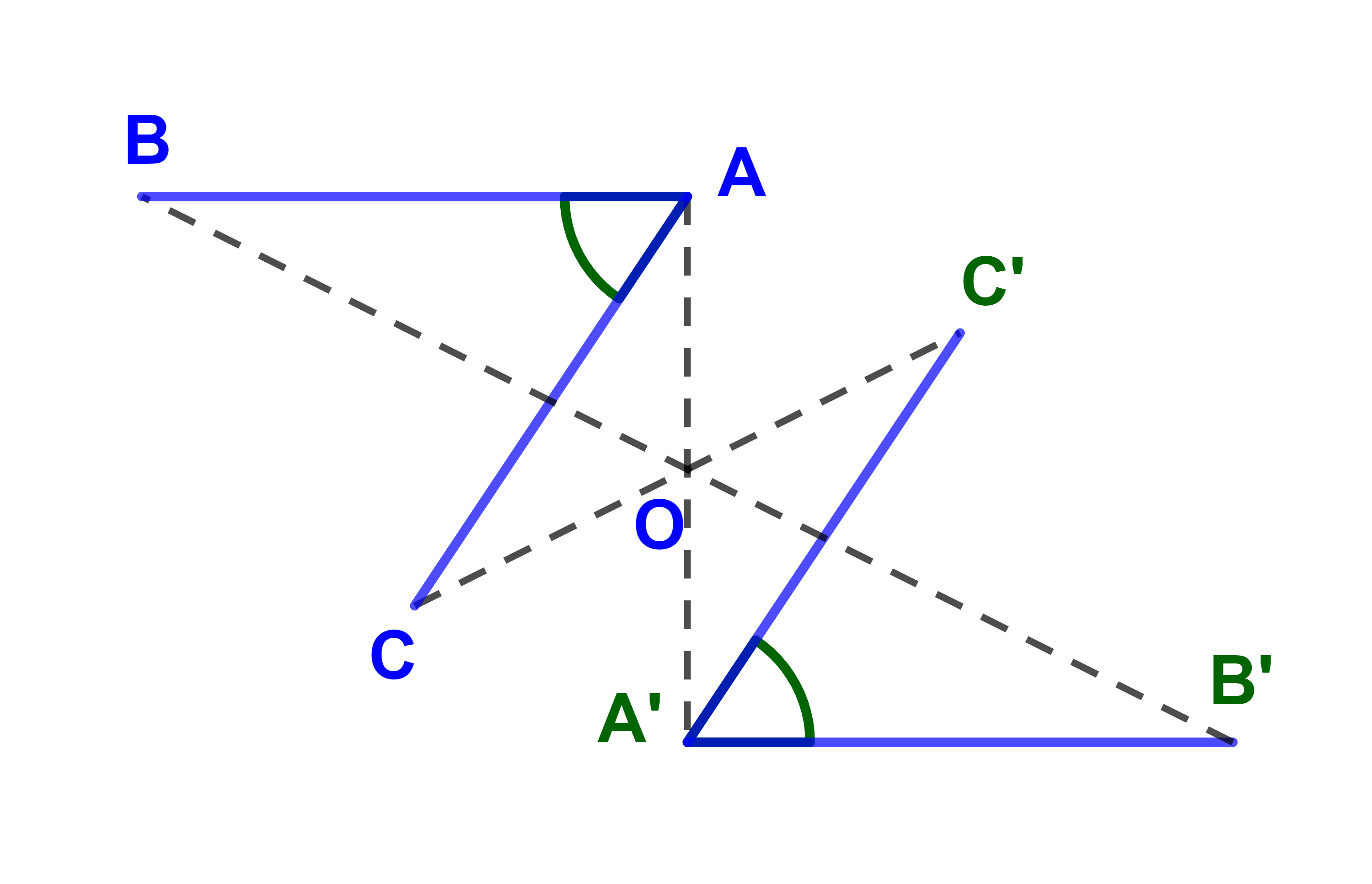
1.3.2 Propriété
Soient F1 et F2 deux figures dont les images sont respectivement F'1 et F'2 par une symétrie centrale T.
Si F1 et F2 se coupent en A alors F'1 et F'2 se coupent en A' tel que A'=T(A).