2 La symétrie axiale

2.1 Définition et Représentation

2.1.1 Définition

Soit D une droite dans le plan.
La transformation géométrique reliant chaque point M du plan au point M' tel que (D) soit la médiatrice du segment [MM'] est appelée symétrie axiale d'axe (D) et est notée S_D.

Autrement dit: S_(D)(M)=M' signifie (D)⊥(MM') au milieu du segment [MM'].

2.1.2 Représentation graphique

Soit M un point et S_D(M)=M'.

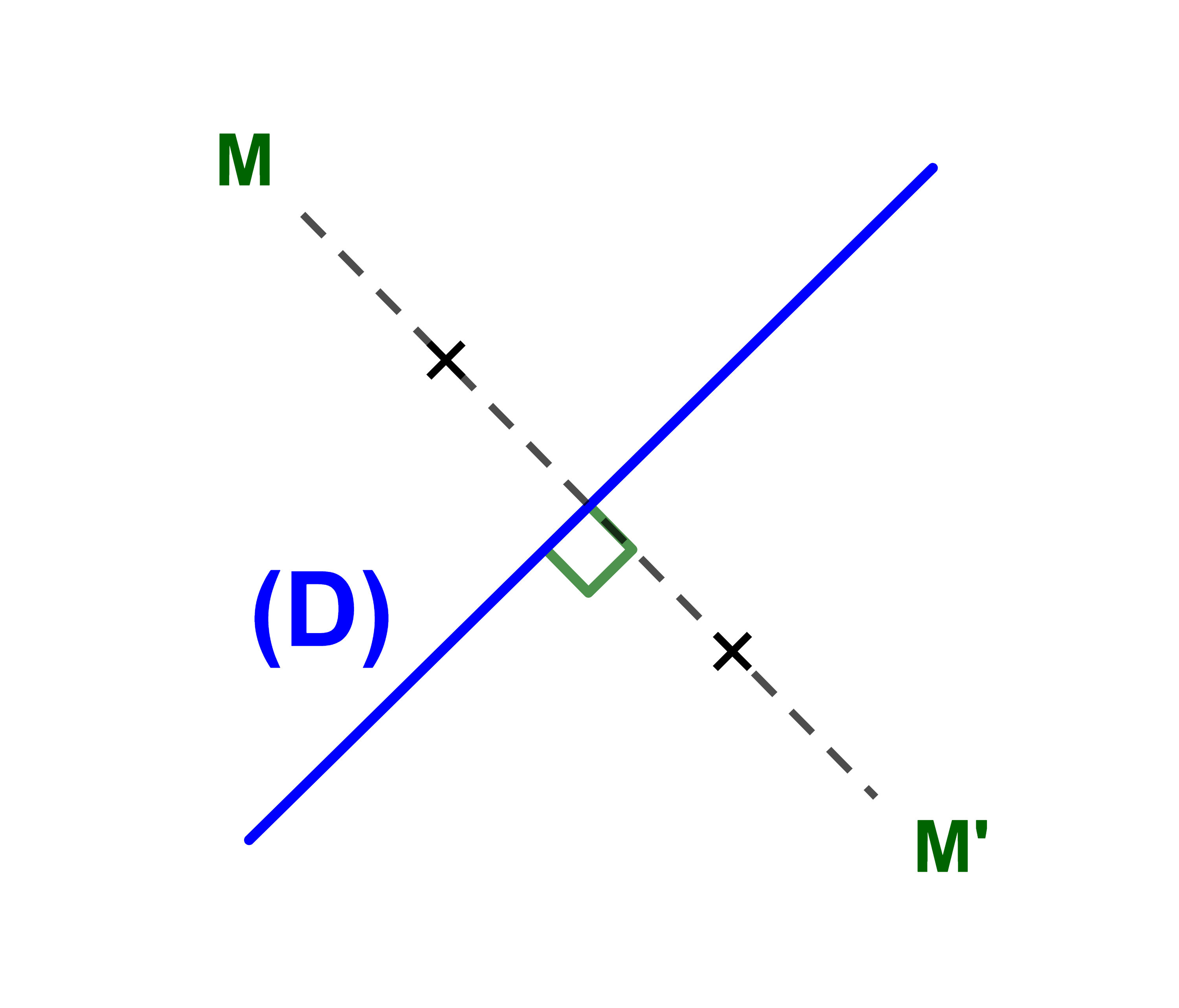
Remarque
1) L'image d'un point de l'axe (D) est lui même
on dit la droite (D) est invariante par la symétrie axiale S_(D).
2) Si (D')⊥(D) alors (D') est globalement invariante par S_(D)
mais le seul point de (D') invariant par S_(D) est le point d'intérsection de (D) et (D').

2.2 Conservation du coefficient de colinéarité de deux vecteurs

2.2.1 Propriété

La symétrie axiale conserve le coefficient de colinéarité de deux vecteurs.

2.2.2 Résultat

La symétrie axiale conserve l'alignement des points et le milieu d'un segment.

2.2.3 Distance et symétrie axiale

Propriété
Soit S une symétrie centrale. La distance de deux points est la même que la distance de leurs symétriques (par rapport à l'axe).
En d'autre terme
si S(A)=A' et S(B)=B' alors A'B'=AB.

Résultat
La symétrie axiale conserve la distance.