3- الازاحة

3.1 تعريف وتمثيل مبياني

3.1.1 تعريف

لتكن u^→ متجهة.
التحويل الهندسي الذي يربط كل نقطة M من المستوى بنقطة M' بحيث MM'^→=u^→ يسمى ازاحة متجهتها u^→ ونرمز لها ب t_u^→.

بتعبير آخر t_u^→(M)=M' يعني MM'^→=u^→.

3.1.2 التمثيل المبياني

لتكن M نقطة و M' صورتها بازاحة t_u^→.

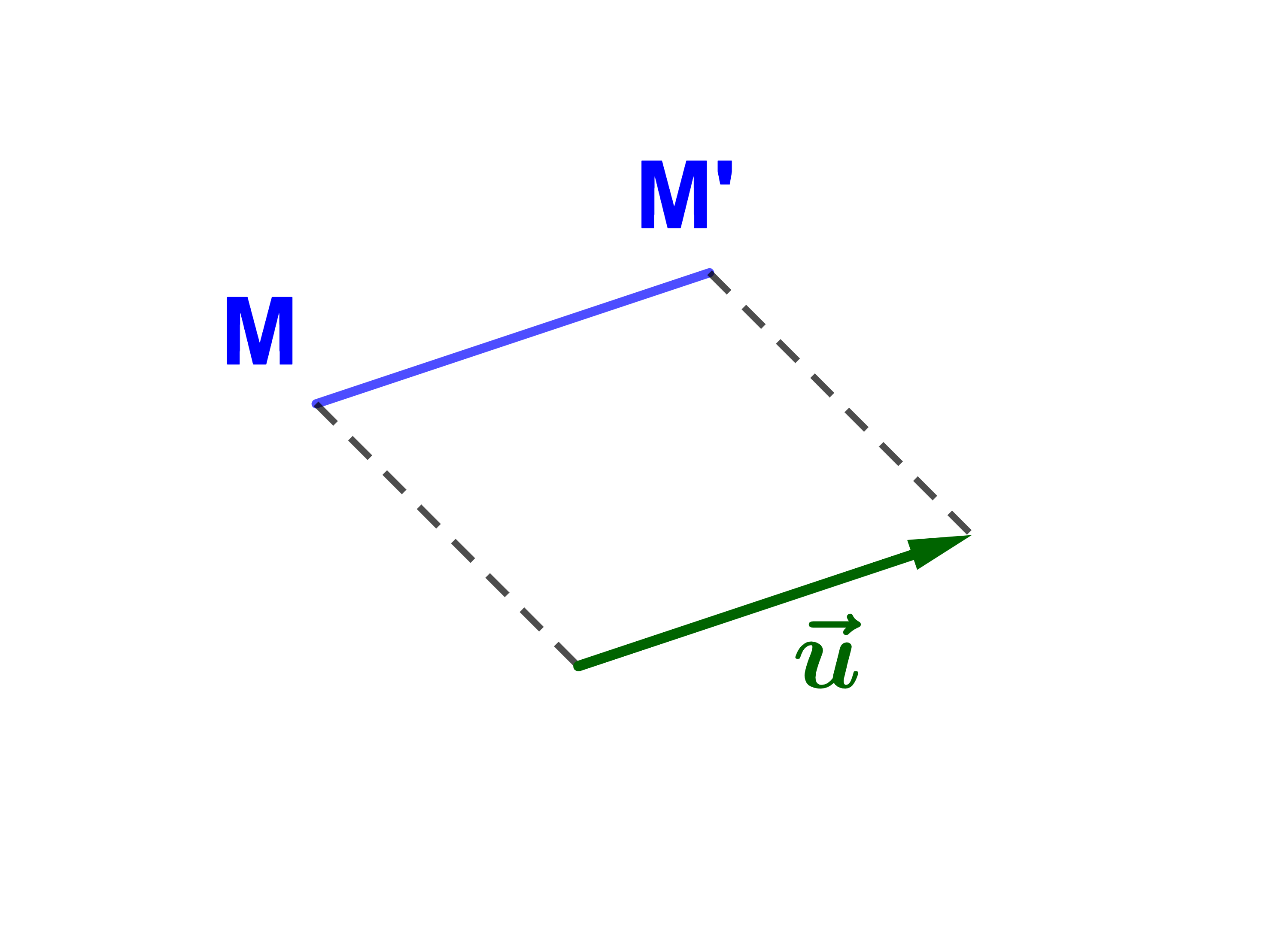
ملاحظة
اذا كانت u^→=AB^→ و t_u^→(M)=M' فان MM'BA متوازي أضلاع

تمرين 1 tp

ليكن EFG مثلثا.
انشئ صورة المثلث EFG بالازاحة دات المتجهة 2FG^→.

3.1.3 الخاصية المميزة لازاحة

يكون تحويل T ازاحة اذا وفقط اذا كان لكل نقطتين M و N لدينا M'N'^→=MN^→
بحيث M'=T(M) و N'=T(N).

تمرين 2 tp

ليكن EFGH متوازي اضلاع مركزه O و T تحويلا يربط كل نقطة M بنقطة M' حيث
MM'^→-2ME^→+MF^→+MH^→=O^→.
1) حدد وانشئ E' و F' و H' صور E و F و H بالتحويل T على التوالي.
2) بين ان التحويل T ازاحة دات المتجهة u^→=2OE^→.

3.4 الحفاظ على معامل استقامية متجهتين

3.4.1 تقديم

1) u^→ و v^→ مستقيميتان يعني يوجد عدد حقيقي k بحيث v^→=ku^→.
2) توجد ثلاث نقط A و B و C بحيث u^→=AB^→ و v^→=AC^→.
اذن AC^→=kAB^→.

حسب الخاصية المميزة لازاحة
فان A'B^→'=AB^→ و A'C'^→=AC^→
اذن A'C'^→=kA'B'^→, المعامل k لا يتغير.

3.4.2 خاصية

الازاحة تحافظ على معامل استقامية متجهتين.

نتيجة
الازاحة تحافظ على استقامية النقط وعلى منتصف قطعة.