3 La translation

3.1 Définition et Représentation

3.1.1 Définition

Soit u^→ un vecteur. La transformation géométrique reliant chaque point M du plan au point M' tel que MM'^→=u^→ est appelée translation de vecteur u^→ et est notée t_u^→.

Autrement dit: t_u^→(M)=M' signifie MM'^→=u^→.

3.1.2 Représentation graphique

Soit M un point et t_u^→(M)=M'.

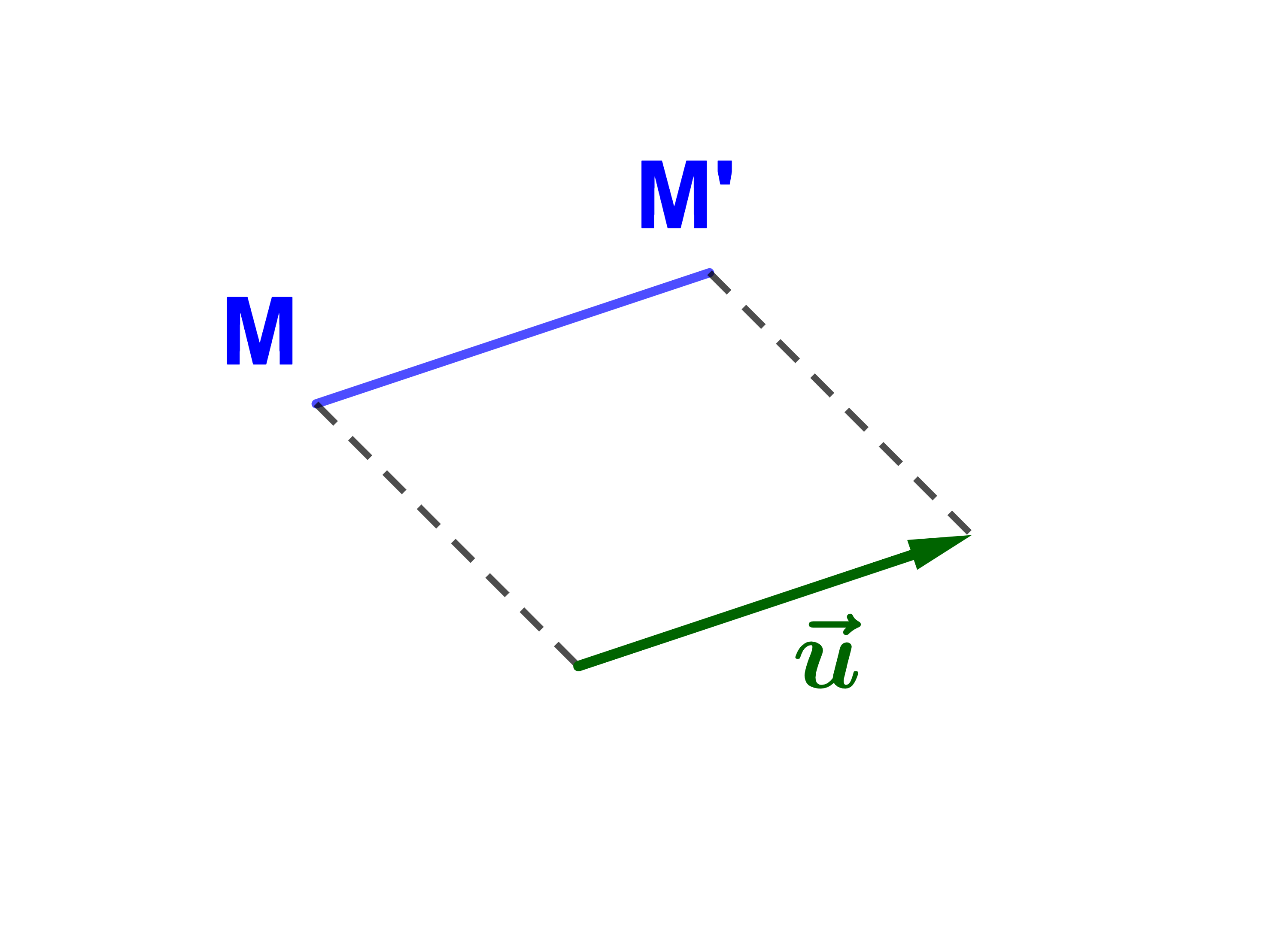
Remarque
Si u^→=AB^→ et t_u^→(M)=M' alors MM'BA est un parallélogramme.

Exercice 1 tp

Soit EFG un triangle.
Tracer l'image du triangle EFG par la translation de vecteur 2FG^→.

3.1.3 Propriété caractéristique d'une translation

Une transformation T est une translation si et seulement si tous points M et N on a
M'N'^→=MN^→ tels que M'=T(M) et N'=T(N).

Exercice 2 tp

Soit EFGH un parallélogramme de centre O et T la transformation reliant chaque point M du plan au point M' tel que
MM'^→-2ME^→+MF^→+MH^→=O^→.
1) Déterminer et tracer les points E'; F' et H' des images respectivement des points E ; F et H par T.
2) Montrer que la transformation T est une translation du vecteur u^→=2OE^→.

3.4 Conservation du coefficient de colinéarité de deux vecteurs

3.4.1 Introduction

1) Deux vecteurs u^→ et v^→sont colinéaires signifie qu'il existe un réel k tel que v^→=ku^→.
2) Il existe trois points A ; B et C tels que
u^→=AB^→ et v^→=AC^→
Donc AC^→=kAB^→.

En utilisant la Propriété caractéristique de la translation on obtient
A'B^→'=AB^→ et A'C'^→=AC^→
ainsi A'C'^→ = kA'B'^→.

3.4.2 Propriété

La translation conserve le coefficient de colinéarité de deux vecteurs.

Résultat
La translation conserve l'alignement des points et le milieu d'un segment.