4- التحاكي

4.1 تعريف وتمثيل مبياني

4.1.1 تعريف

لتكن W نقطة من المستوى و k∈IR*
التحويل الهندسي الذي يربط كل نقطة M من المستوى بنقطة M' بحيث O منتصف القطعة WM'^→=kWM^→ يسمى تحاك مركزه W ونسبته k ونرمز له ب h.

بتعبير آخر h(M)=M' يعني WM'^→=kWM^→.

4.1.2 نتائج

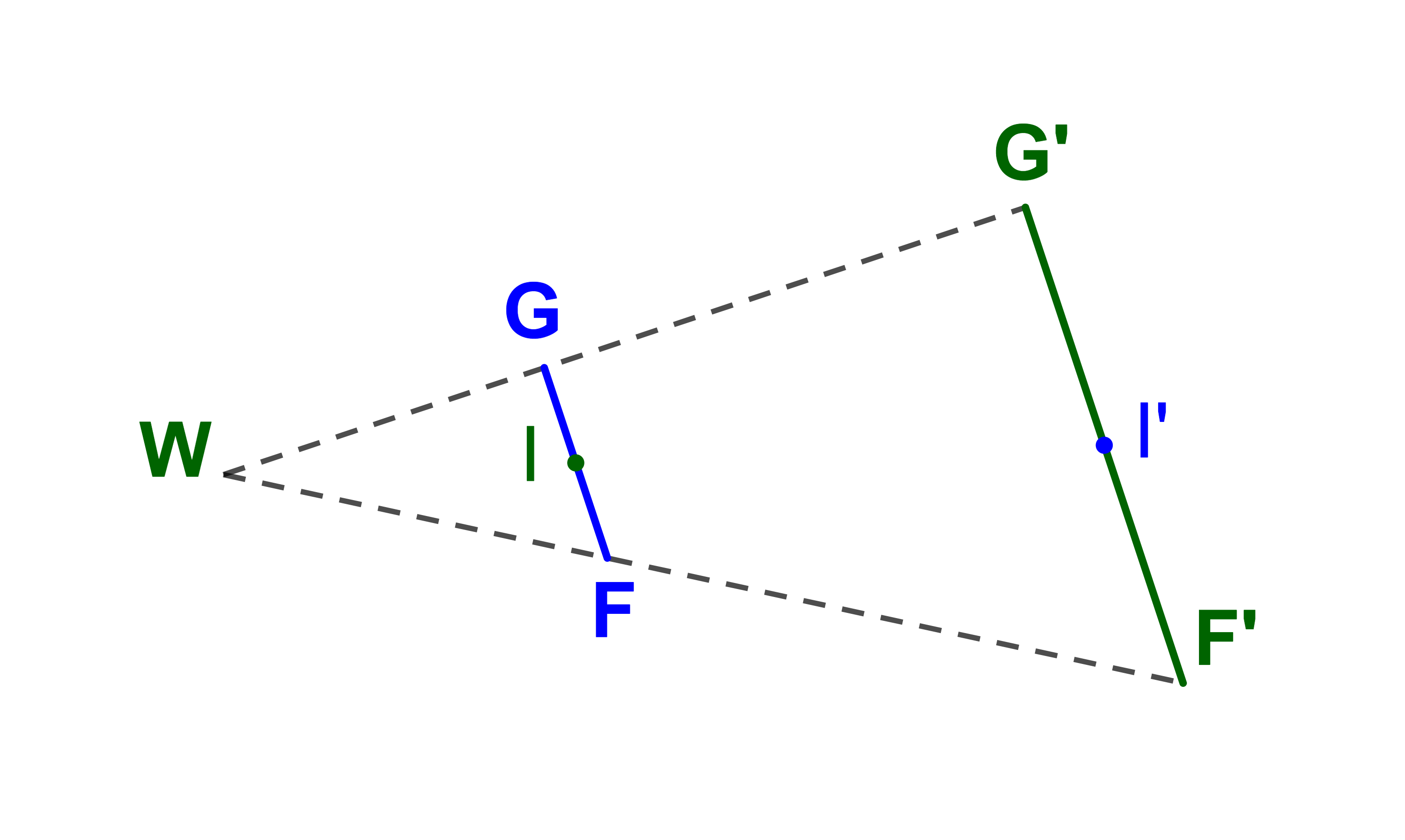
ليكن h تحاك مركزه W. نعتبر نقطة M من المستوى وصورتها ب M' بواسطة h.
1) النقط W و M و M' ستقيمية.
2) التحاكي h يقبل نقطة صامدة واحدة وهي مركزه.

ملاحظة
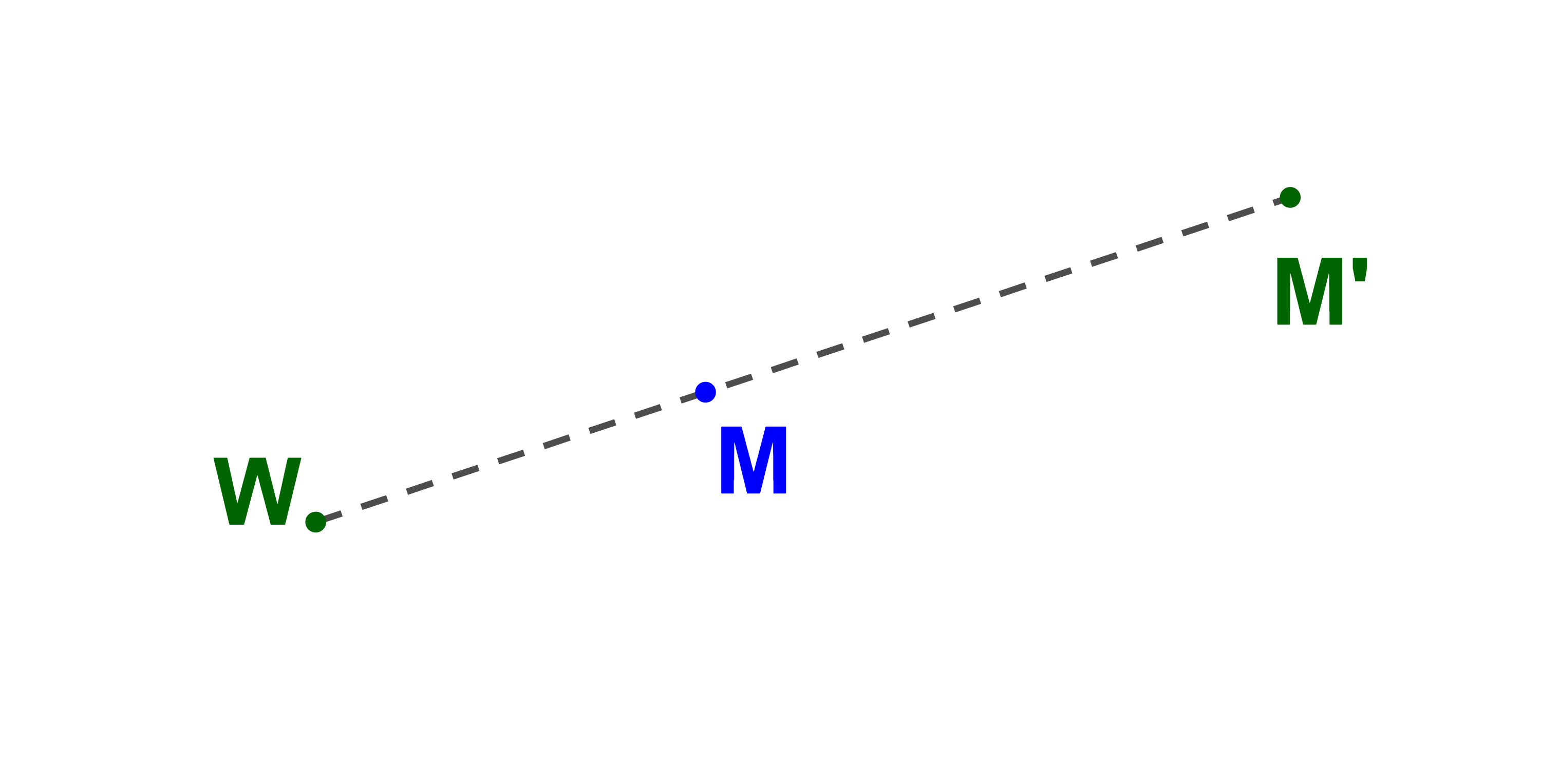
التماثل المركزي الذي مركزه W هو تحاك مركزه W ونسبته -1.

4.1.3 الخاصية المميزة لتحاك

يكون تحويل T تحاك نسبته k اذا وفقط اذا كان لكل نقطتين M و N
لدينا M'N'^→=kMN^→ بحيث M'=T(M) و N'=T(N).

تمرين

تمرين 1 tp

لتكن E و F نقطتين من المستوى و T تحويلا يربط كل نقطة M من المستوى بنقطة M' بحيث
ME^→+MF^→-3MM'^→=O^→.
1) انشئ T(E) و T(F)
2) بين ان T تقبل نقطة صامدة I.
3) حدد طبيعة التحويل T.

4.2 الحفاظ على معامل استقامية متجهتين

4.2.1 تقديم

1) u^→ و v^→ متجهتان مستقيميتان يعني يوجد عدد حقيقي t بحيث v^→=tu^→.
2) توجد ثلاث نقط A و B و C بحيث
u^→=AB^→ و v^→=AC^→
اذن AC^→=tAB^→

حسب الخاصية المميزة لتحاك نسبته k
فان A'B^→'=kAB^→ و A'C'^→=kAC^→, ومنه فان A'C'^→=tA'B'^→ المعامل t لا يتغير.

4.2.2 خاصية

التحاكي يحافظ على معامل استقامية متجهتين.

4.2.3 نتائج

التحاكي يحافظ على استقامية النقط ويحافظ على منتصف قطعة.