4- L’homothétie

4.1 Définition et Représentation

4.1.1 Définition

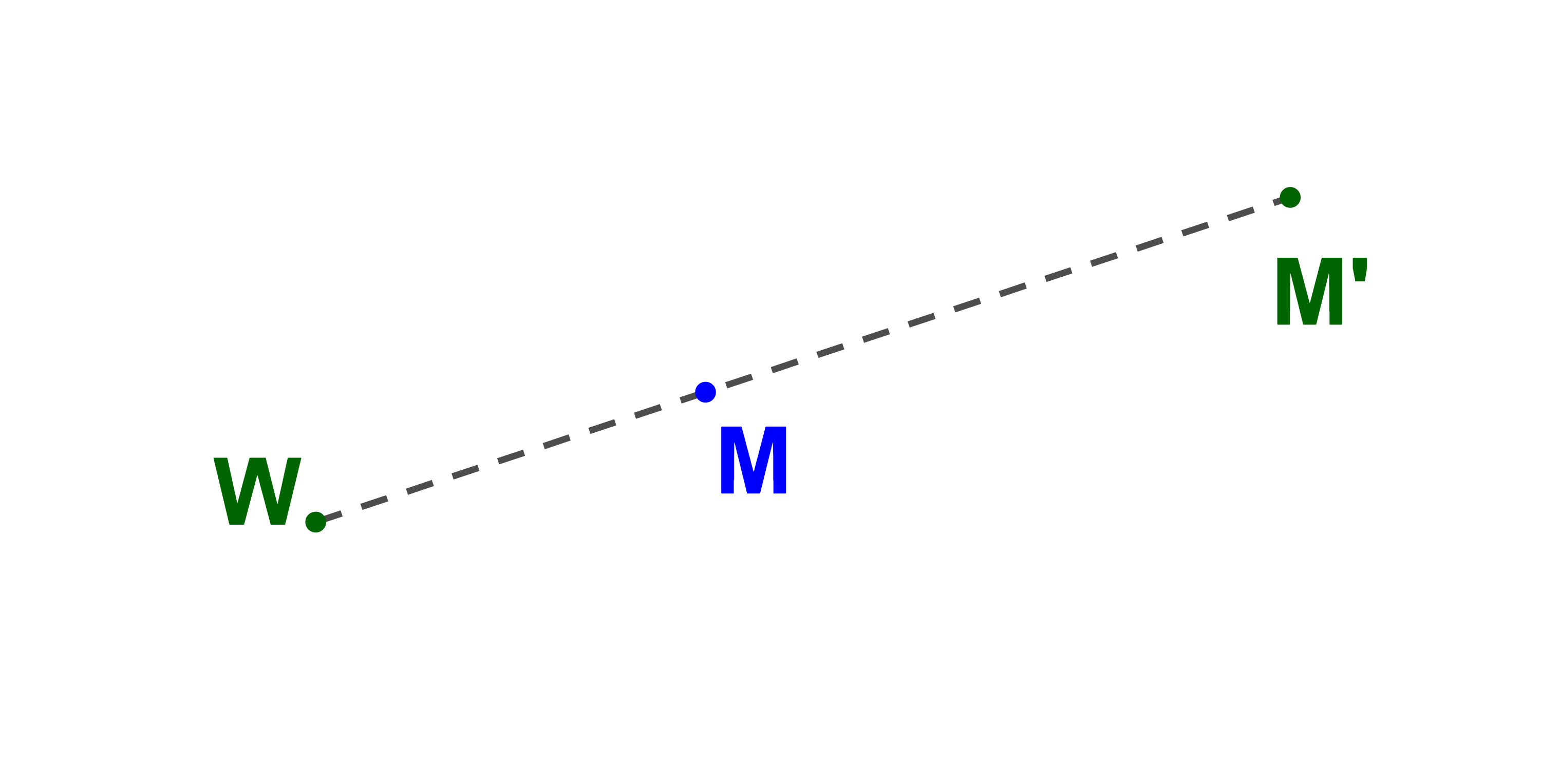
Soit W un point dans le plan et k∈IR*. La transformation géométrique reliant chaque point M du plan au point M' tel que WM'^→=kWM^→
O est appelée homothétie de centre W et de rapport k.

Autrement dit: h(M)=M' signifie WM'^→=kWM^→.

4.1.2 Résultats

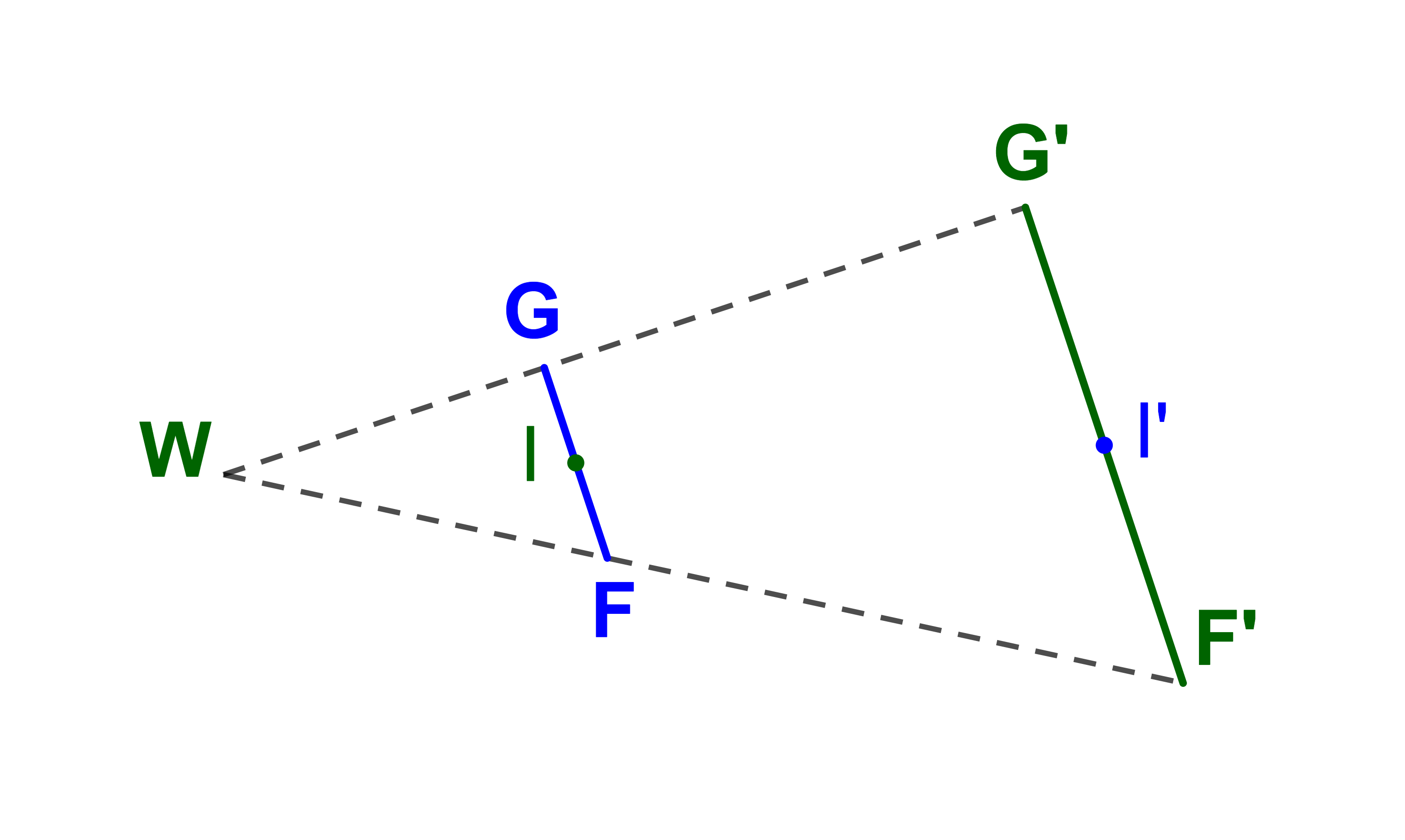
Soit h une homothétie de centre W. On considère un point M et son image M' par h.
1) Les points W , M et M' sont alignés.
2) L'homothétie h admet un seul point invariant (le centre W).

Remarque
Une symétrie cenrale de centre W est une homothétie de centre W et de rapport -1.

4.1.3 Propriété caractéristique d'une homothétie

Une transformation T est une homothétie de rapport k si et seulement si tous points M et N
on a M'N'^→=kMN^→
tels que M'=T(M) et N'=T(N).

Exercice 1 tp

Soient E et F deux points du plan et T la transformation reliant chaque point M du plan au point M' de façon que
ME^→+MF^→-3MM'^→=O^→.
1) Tracer T(E) et T(F).
2) Montrer que T admet un point invariant I.
3) Déterminer la nature de la transformation T.

4.2 Conservation du coefficient de colinéarité de deux vecteurs

4.2.1 Introduction

1) Deux vecteurs u^→ et v^→sont colinéaires signifie qu'il existe un réel t tel que v^→=tu^→.
2) Il existe trois points A; B et C tels que
u^→=AB^→ et v^→= AC^→
donc AC^→=tAB^→.

En utilisant la Propriété caractéristique de l'homothétie de rapport k on obtient
A'B^→'=kAB^→ et A'C'^→=kAC^→, ainsi A'C'^→=tA'B'^→.

4.2.2 Propriété

L'homothétie conserve le coefficient de colinéarité de deux vecteurs.

4.2.3 Résultat

L'homothétie conserve l'alignement des points et le milieu d'un segment.