تمرين 1 tp

ليكن x∈IR.
بين أن cos⁴x-sin⁴x=-1+2cos²x.

تصحيح

التعبير cos⁴x-sin⁴x تطابقة هامة.
cos⁴x-sin⁴x=(cos²)²x-(sin²)²x
=(cos²x-sin²x)(cos²x+sin²x)
لدينا cos²x+sin²x=1 اذن sin²x=1-cos²x ومنه فان
cos²x-sin²x=cos²x-(1-cos²x)=-1+2cos²x.
وبالتالي cos⁴x-sin⁴=-1+2cos²x.

تمرين 2 tp

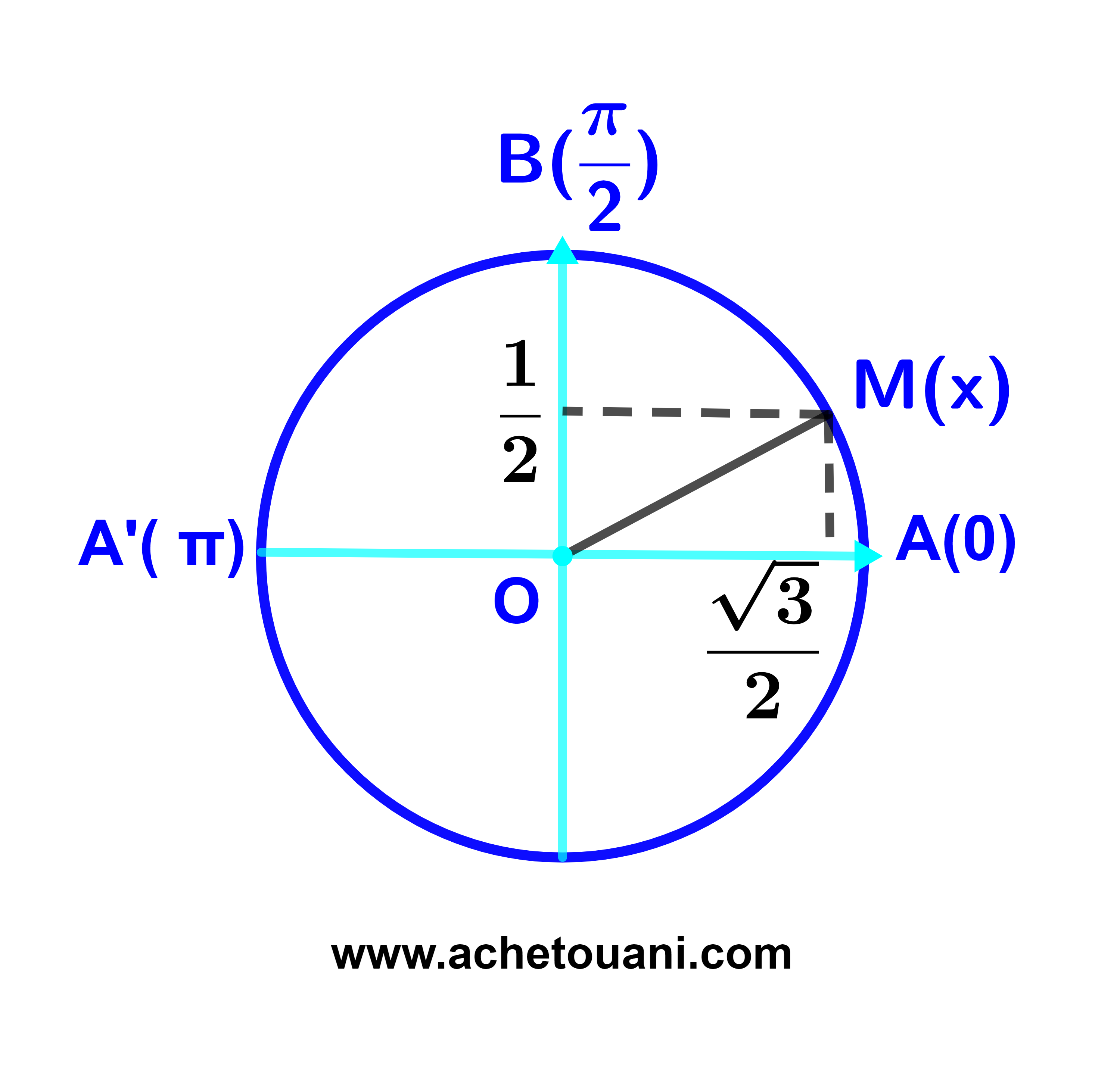
1) أنشئ النقكة M(x) على الدائرة المثلثية (C) بحيث

sinx =	1	; x∈I = [0 ;	π	]
	2		2

2) أحسب cosx و tanx علما أن x∈I.

تصحيح

1) M(x)∈(C) يعني أن sinx أرتوب النقطة M في المعلم المرتبط بالدائر المثلثية (C) و cosx أفصولها
وبالتالي M(cosx;sinx).

2) لدينا cos²x+sin²x=1 أي cos²x=1-sin²x

أي

cos²x = 1 - (	1	)² =	3
	2		4

اذن

cosx =	- √(3)	أو	cosx =	√(3)
	2			2

M∈arc[AB] اذن cosx ≥ 0

cosx =	√(3)	وبالتالي
	2

لدينا cosx≠0 اذن tanx∈IR

tanx =	sinx
	cosx

أي

tanx =		1
		2
		√(3)
		2

لدينا اذن

tanx =	√(3)
	3

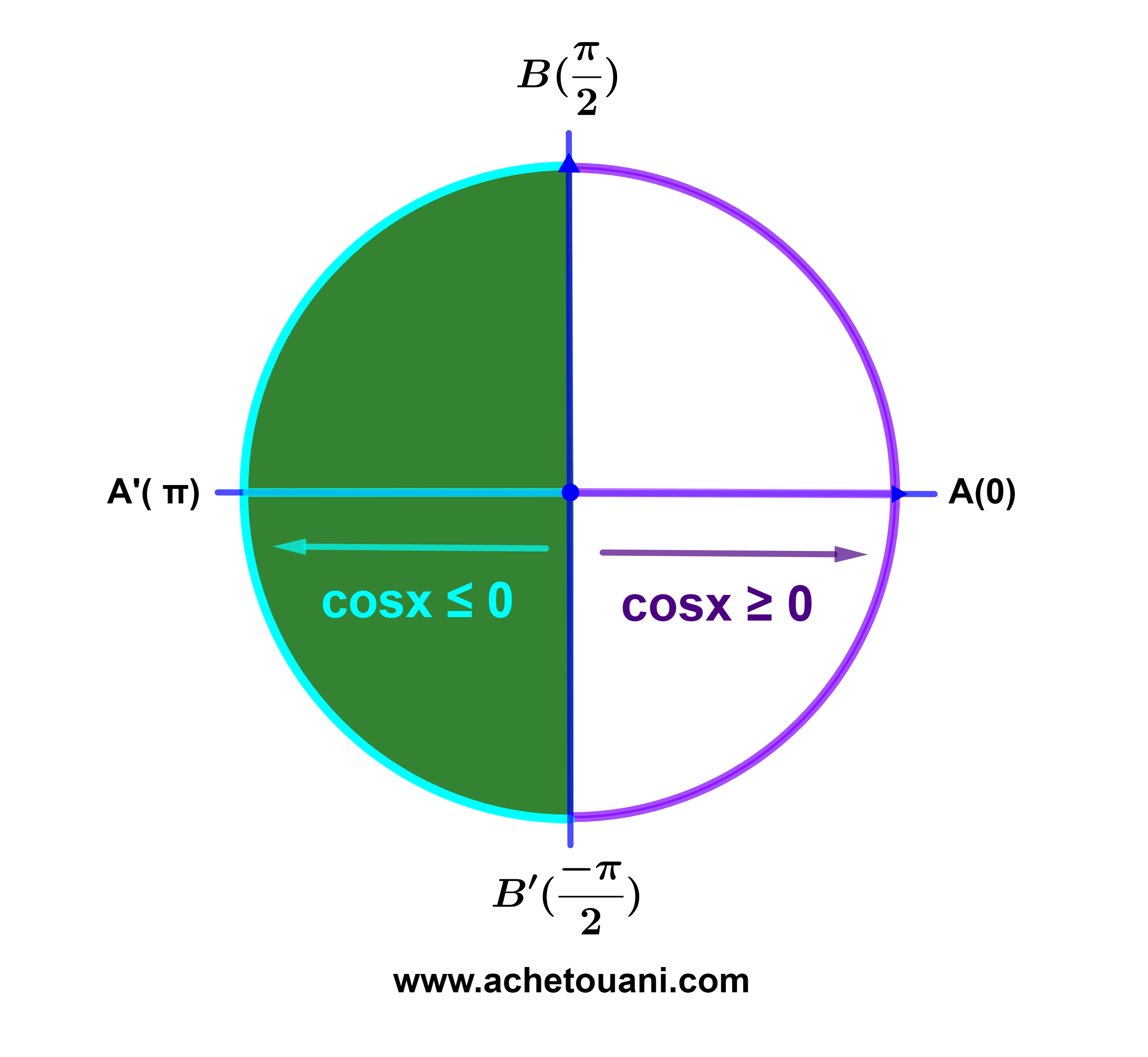
5.1.4 خاصية 3

1) Si x∈[	-π	;	π	]
	2		2

فان cosx≥0.

2) si x∈[-π;	-π	] ∪ [	π	; π]
	2		2

فان cosx≤0.

5.1.5 خاصية 4

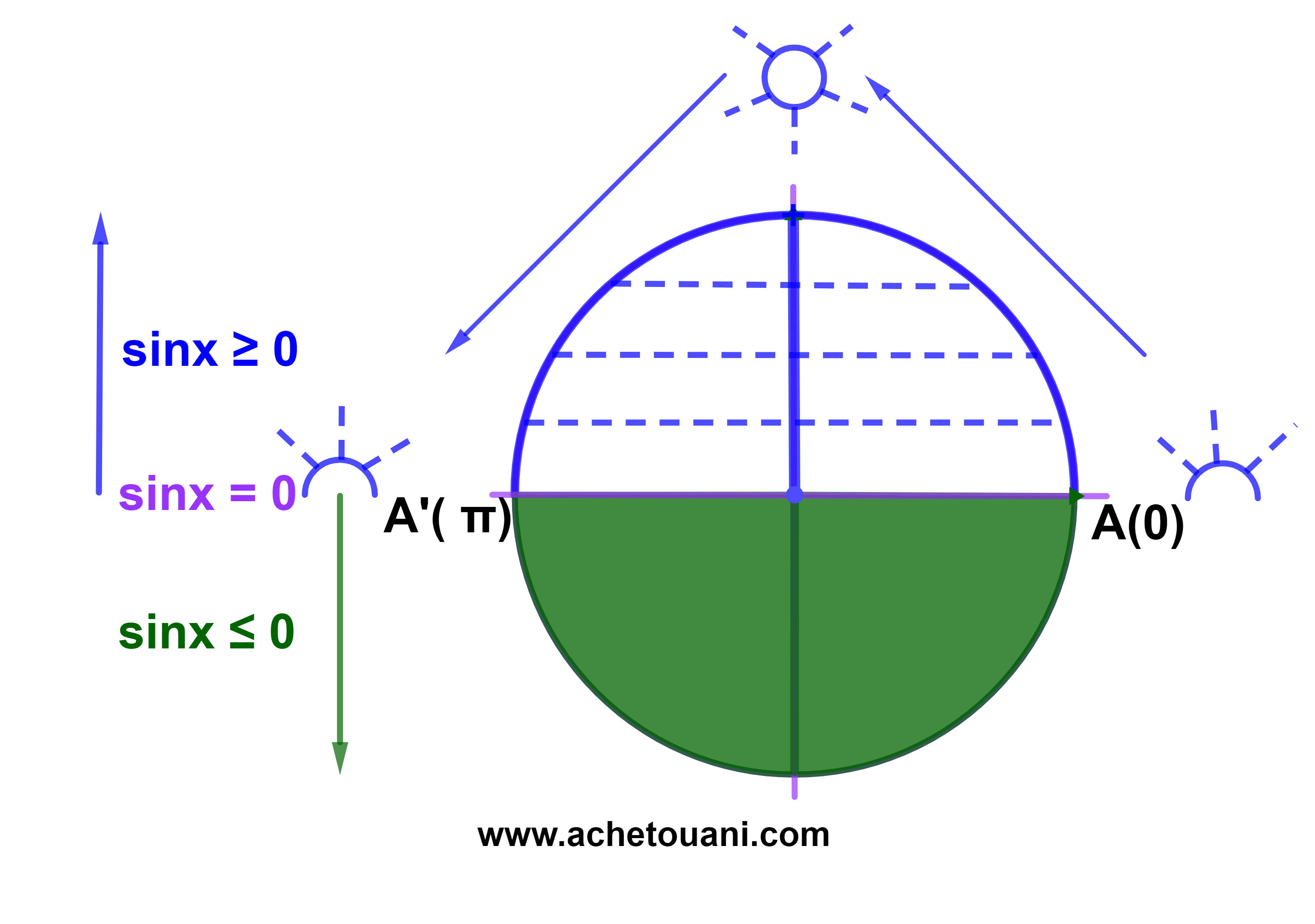
1) اذا كان x∈[-π;0] فان sinx≤0.
2) اذا كان x∈[0;π] فان sinx≥0.