4- الخطوط المثلثية لعدد حقيقي وزاوية متجهتين

4.1 الخطوط المثلثية لعدد حقيقي

(C) دائرة مثلثية ومرتبطة بالمعلم المتعامد الممنظم المباشر (O;i^→;j^→).
لكل عدد حقيقي x توجد نقطة وحيدة M(x) من الدائرة (C) صورة العدد x.

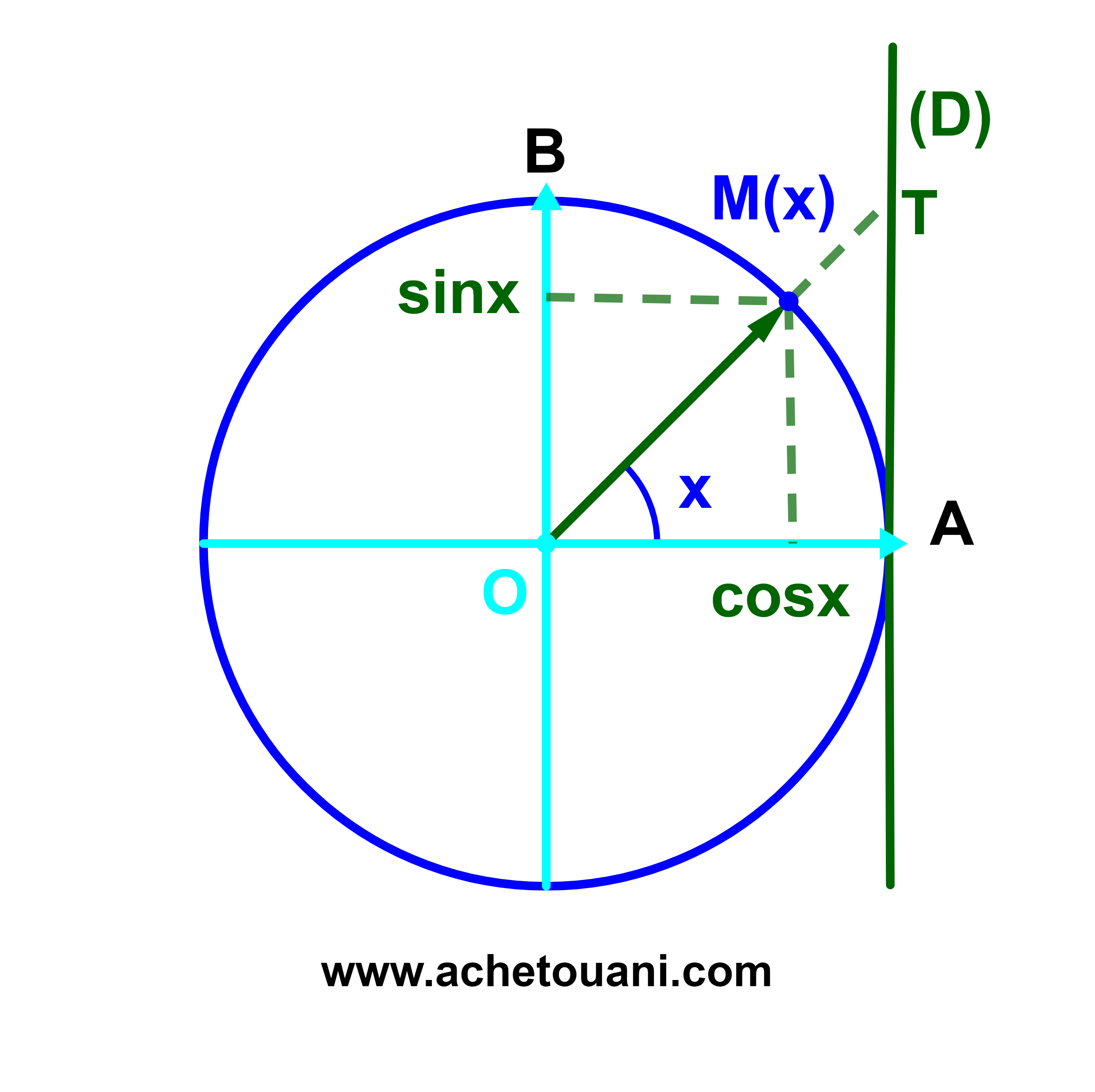
1) أفصول النقطة M في المعلم يسمى cosinus ل x ونرمز له ب cosx.
2) أرتوب النقطة M في المعلم يسمى sinus ل x ونرمز له ب sinx.
3) اذا كان أفصول النقطة T في المحور (D) موجودا فانه يسمى tangente ل x ونرمز له ب tanx .

ملاحظة اذا كان (OM)=(OB)
فان T لا توجد لأن (OB)||(D).
وبالتالي tanx يكون معرفا اذا كان x≠(π/2)+kπ بحيث k∈ℤ.

4.2 الخطوط المثلثية لزاوية متجهتين

4.2.1 تعريف

لتكن u^→ و v^→ متجهتين. اذا كان x قياسا بالراديان للزاوية الموجهة (u^→;v^→) فان

{	cos(u→;v→) =	cosx
	sin(u→;v→) =	sinx

5- العلاقات المثلثية والخطوط المثلثية

5.1 العلاقات المثلثية

5.1.1 تقديم

نعتبر OHM مثلثا قائم الزاوية في H.
1) باستعمال مبرهنة فيتاغورس نحصل على OH²+HM²=OM²
OM=1 و OH=cosx و HM=OK=sinx
اذن cos²x+sin²x=1.

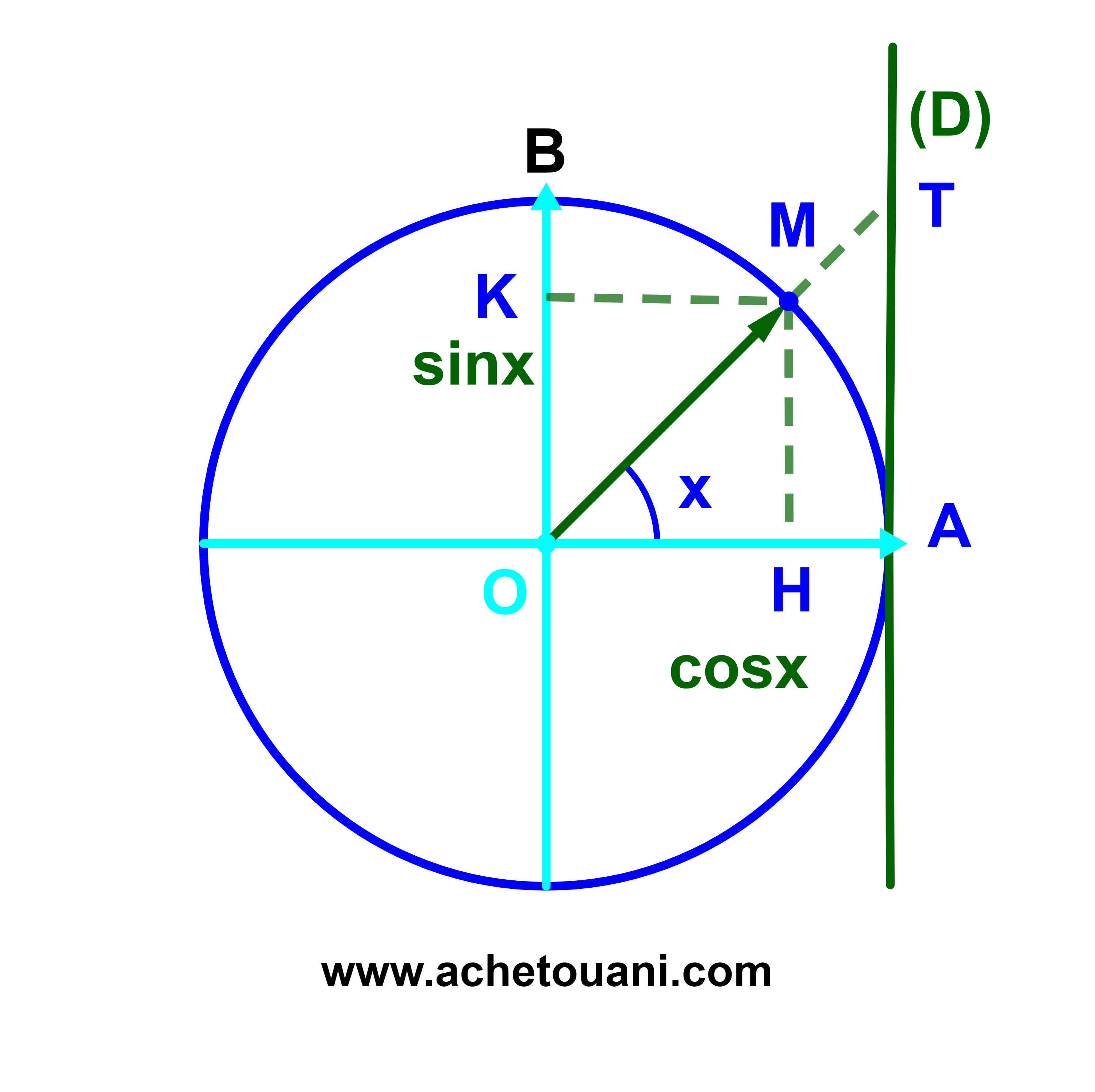
2) tanx

tanx =	AT	=	HM
	OA		OH
=	OK	=	sinx
	OH		cosx

3) العلاقة بين tanx و cosx.

1+tan²x = 1+	sin²x
	cos²x

=	cos²x+sin²x	=	1
	cos²x		cos²x

5.1.2 خاصية 1

ليكن x∈IR. cos²x + sin²x = 1

5.1.3 خاصيات 2

ليكن x∈IR بحيث

k∈ℤ حيث	x≠	π	+kπ
		2

{	tanx =	sinx
		cosx
	1 + tan²x =	1
		cos²x