5.2 الخطوط المثلثية

5.2.1 خاصيات

x		0	π		π		π		π
			6		4		3		2
sinx		0	1		√2		√3		1
			2		2		2
cosx		1	√3		√2		1		0
			2		2		2
tanx		0	√3		1		√3		×
			3

5.3- العلاقات بين الخطوط المثلثية

5.3.1 خاصيات

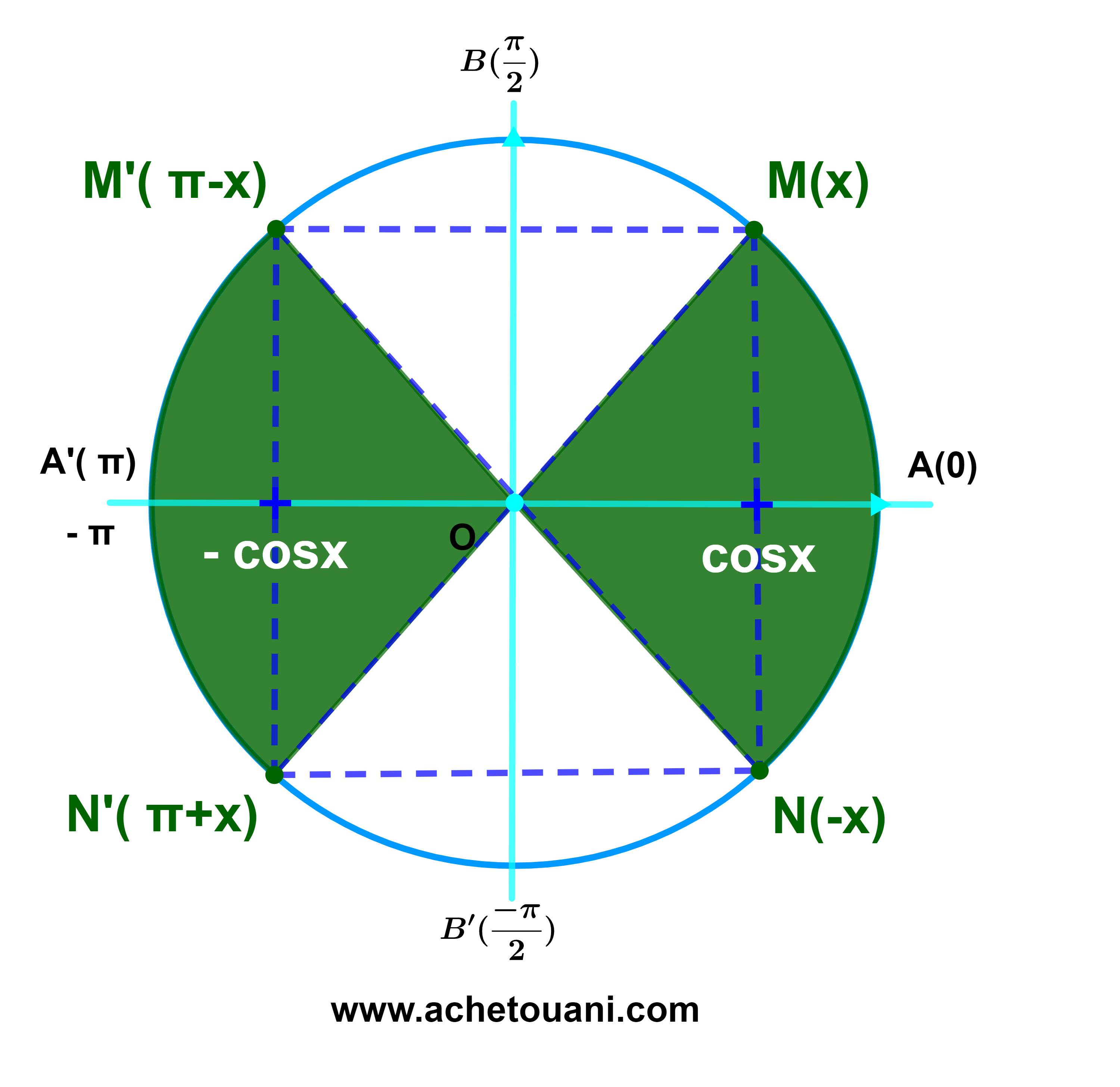
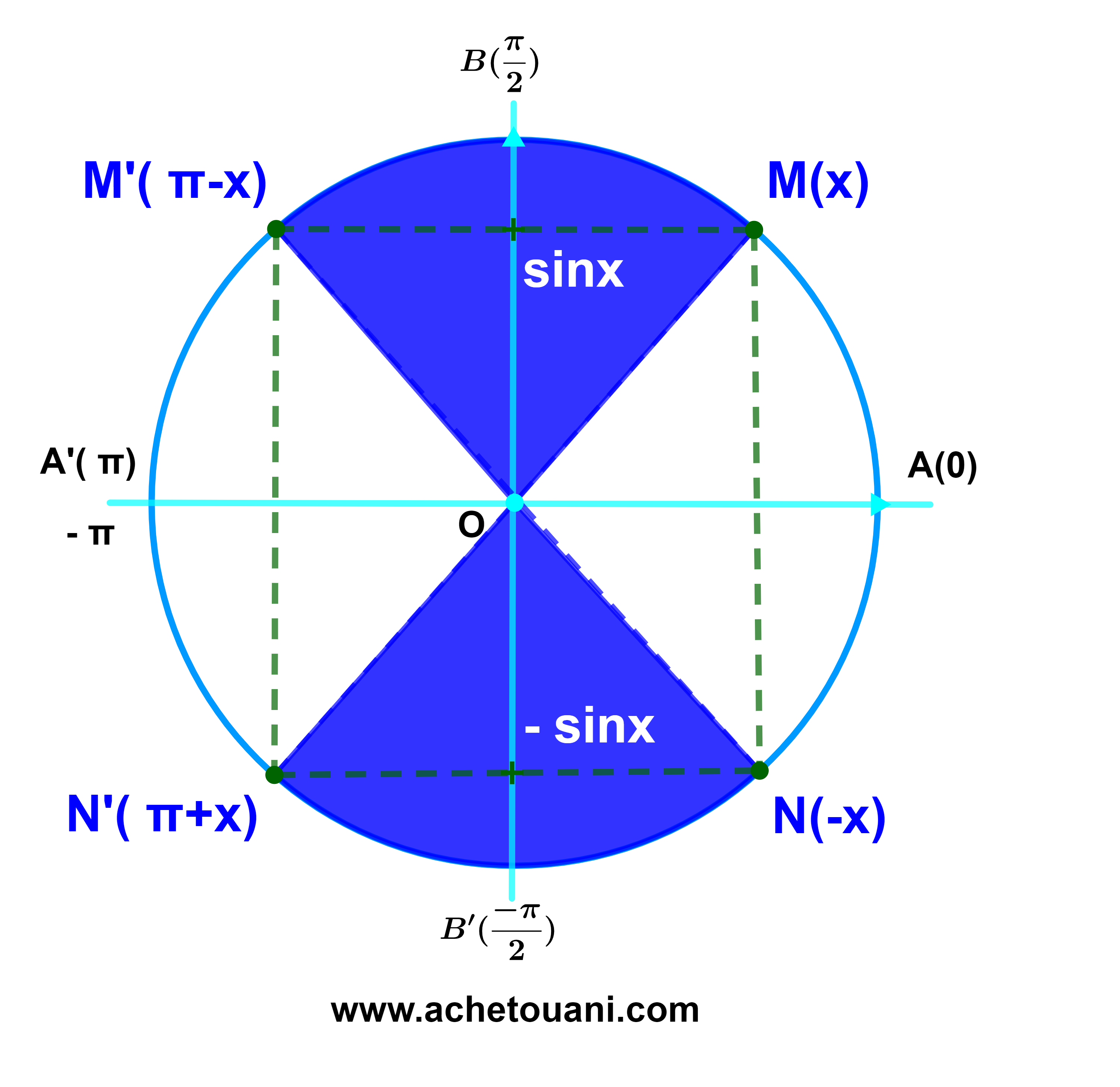
cos(-x) = cosx		sin(-x) = -sinx
sin(x+2kπ) = sinx		cos(x+2kπ) = - cosx
tan(-x) = - tanx		tan(x+kπ) = tanx
sin(π-x) = sinx		cos(π-x)= - cosx
sin(π+x) = - sinx		cos(π+x)= - cosx
tan(π-x) =- tanx		tan(π+x)= tanx

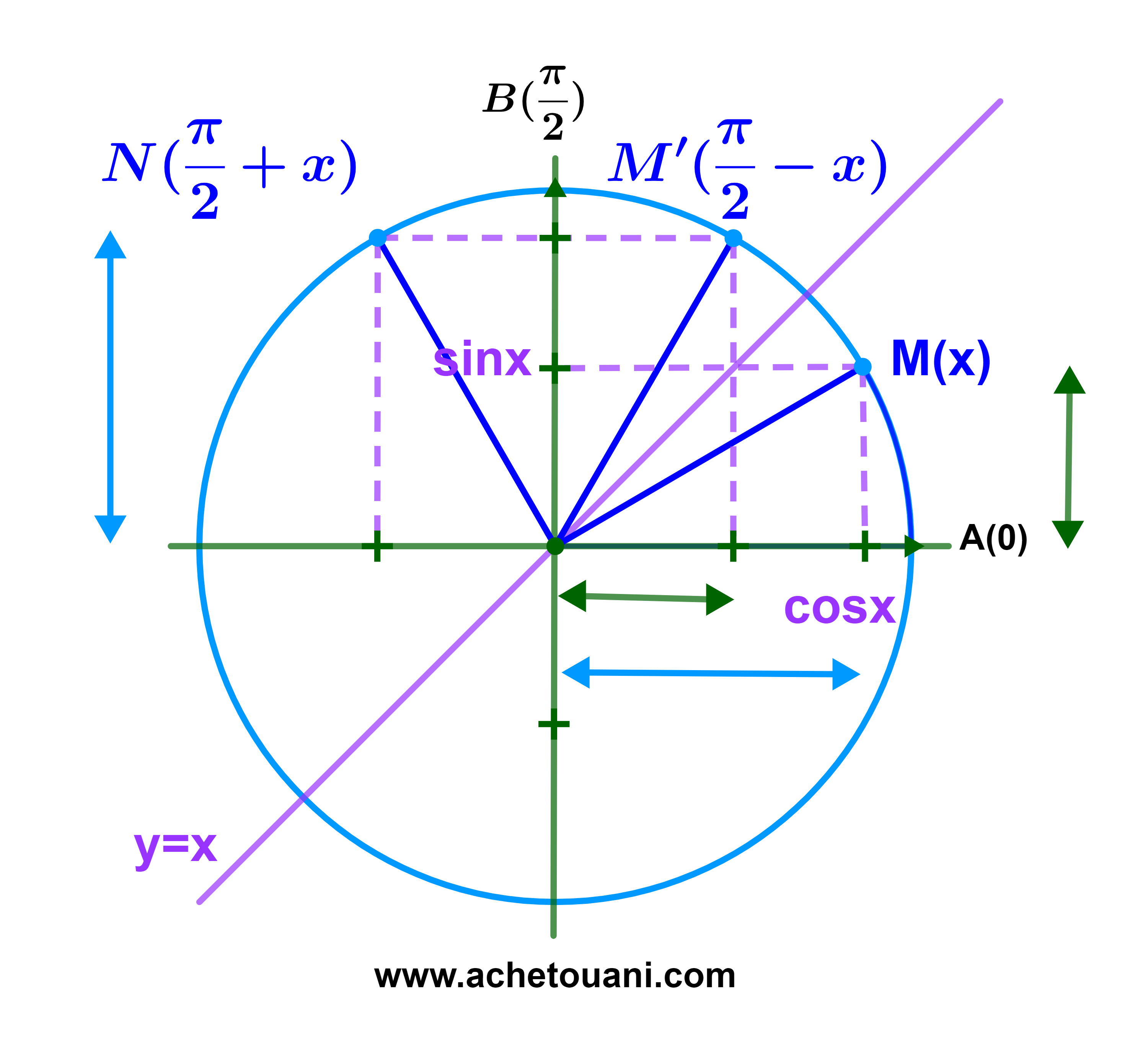
	sin(	π	- x) = cosx
		2
	cos(	π	- x) = sinx
		2
	sin(	π	+ x) = cosx
		2
	cos(	π	+ x) = - sinx
		2

	tan(	π	- x) =	1
		2		tanx
	tan(	π	+ x)=-	1
		2		tanx

تمرين 1 tp

بسط مايلي
A=cos(4π+x)+cos(3π-x).
B=sin(9π-x)+sin(x+8π).
C=tan(3π-x)+tan(4π+x).

تصحيح

A=cos(x+2.2π)+cos(π+2.1π-x).

A=cosx +cos(π-x)=cosx-cosx اذن A=0

B=sin(π+2.4π-x)+sin(x+2.4π).

B=sin(π-x)+sin(x)=sinx+sinx اذن B=2sinx.
C=tan(-x+3π)+tan(x+4π)
=tan(-x)+tan(x)=-tanx+tanx=0
اذن C=0.

تمرين 2 tp

أحسب

cos(	7π	) ; sin(	13π	)
	4		3
tan(	-83π	) ; tan(	2021π	)
	4		3