1 تمرين tp

بين أن الأفاصيل المنحنية التالية

x =	83π		y =	-117π		z =	123π
	4			4			4

تمثل نفس النقطة M على الدائرة المثلثية (C).

تصحيح

للتذكير
x و y أفصولان يمثلان نفس النقطة على الدائرة المثلثية (C) يعني x≡y[2π].

بتعبير آخر
x=y+2kπ بحيث k∈ℤ يعني x و y لهما نفس الأفصول المنحني الرئيسي.

x - y =	83π	-	-117π
	4		4

=	200π	=	2x25π
	4

اذن x=y+2kπ بحيث k=25∈ℤ وبالتالي x و y يمثلان نفس النقطة على (C).

x - z =	83π	-	123π
	4		4
=	-40π	=	2x(-20)π
	4

x=z+2kπ بحيث k=-20∈ℤ وبالتالي x و z يمثلان نفس النقطة على (C).
لدينا اذن x≡y[2π] و x≡z[2π] ومنه فان y≡z[2π] وبالتالي x و y و z تمثل نفس النقطة على (C).

تمرين 2 tp

ليكن x الأفصول المنحني الرئيسي للنقطة M. حدد الأفاصيل المنحنية للنقطة M التي تنتمي الى المجال I في كل من الحالات التالية

x =	π		I=[	34π	;	43π	]
	4			3		3
x =	π		I=[	-33π	;	-13π	]
	5			5		5

تمرين 3 tp

حدد الأفصول المنحني الرئيسي لكل من النقط التالية

E(	41π	) ; F(	-28π	) ; G(	-13π	)
	4		3		3

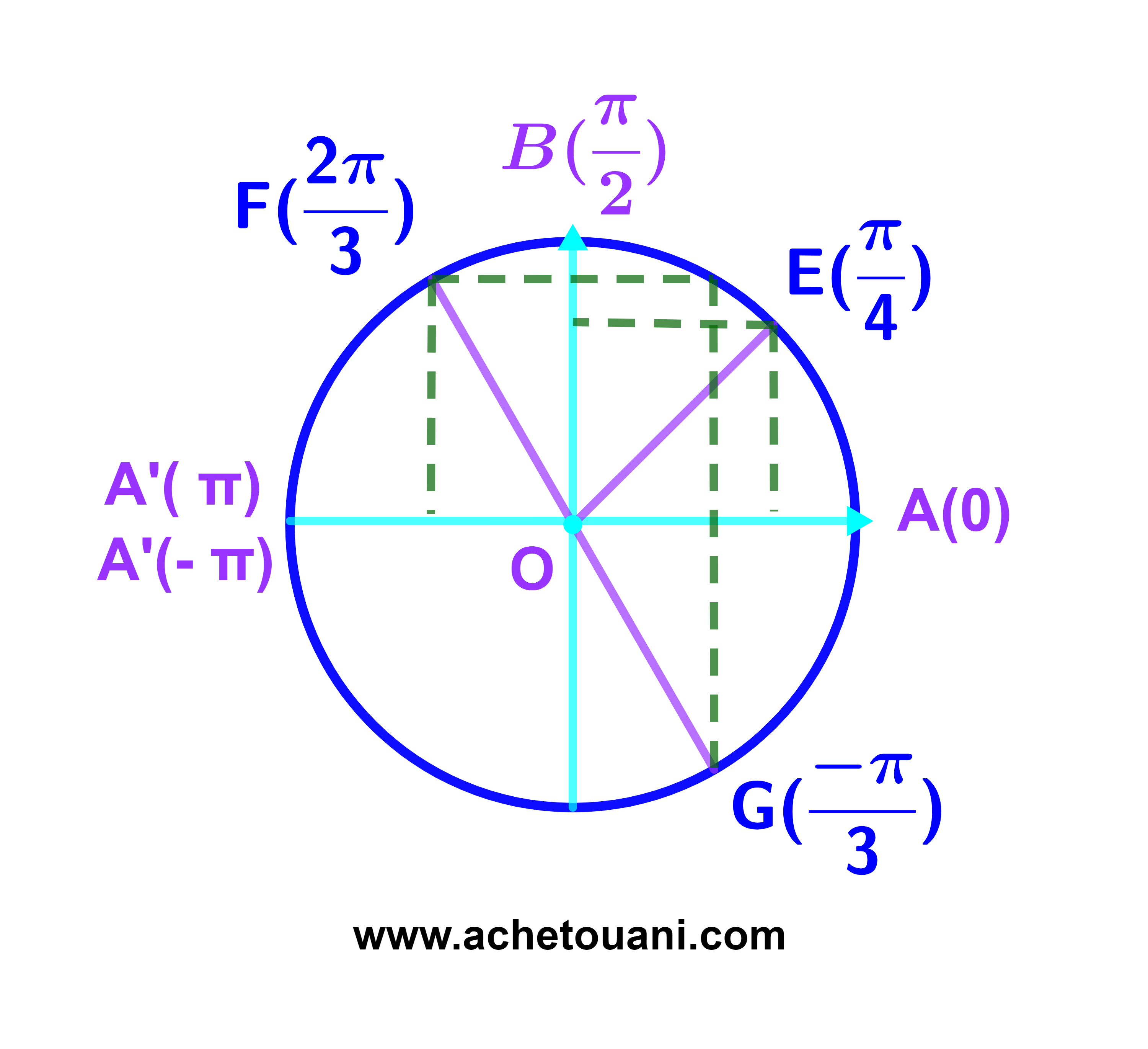
ومثل النقط على الدائرة المثلثية (C).

تصحيح

1) الأفصول الرئسي للنقطة E(a)
41÷4=10,25 و 10 عدد زوجي
اذن 41π=4×10π+π.

a =	4×10π+π	=	π	+ 2×5π
	4		4

a =	π	∈]-π ; π] اذن
	4

هو الأفصول المنحني الرئيسي للنقطة E(a).
2) الأفصول النحني الئيسي للنقطة F(b).
28÷3=9,333.. و 9 عدد فردي
28=3x8+4 لكن 4>3
نأخذ الحالة 28=3x10-2 لأن |-2|<3
اذن -28π=3×(-10)π+2π.

b =	3×(-10)π+2π	=	2π	+ 2×(-5)π
	3		3

b =	2π	∈]-π ; π] وبالتالي
	3

هو الأفصول المنحني الرئيسي للنقطة F(b).
3) الأفصول المنحني الرئيسي للنقطة G(c).

c =	3×(-4)π-π	=	-π	+ 2×(-2)π
	3		3

c =	-π	∈]-π ; π] اذن
	3

c هو اذن الأفصول المنحني الرئيسي للنقطة G(c).