الحساب المثلثي (1_6)
3- الزاوية الموجهة
3.1 الزاوية الموجهة لنصفي مستقيم
3.1.1 تعريف
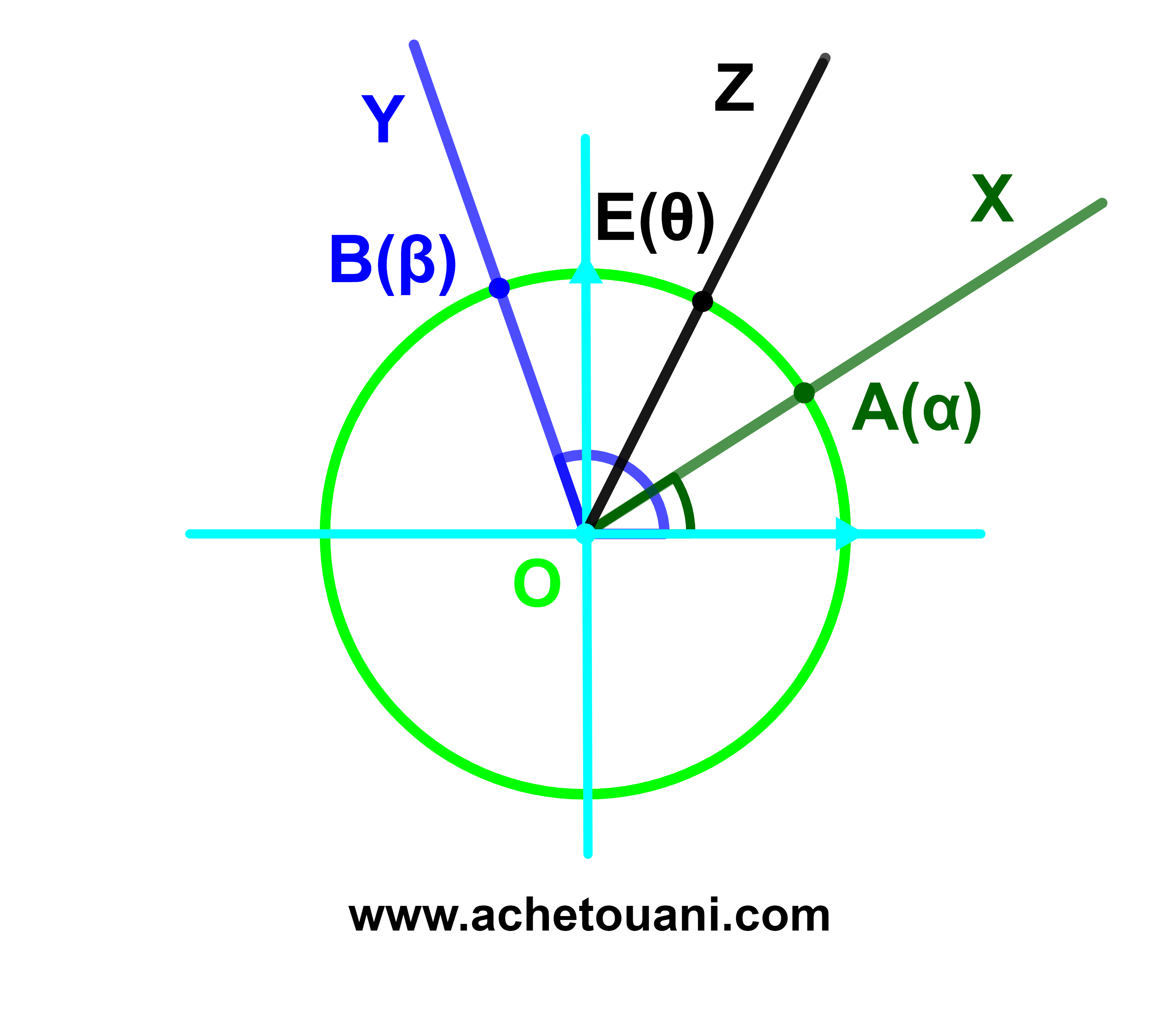
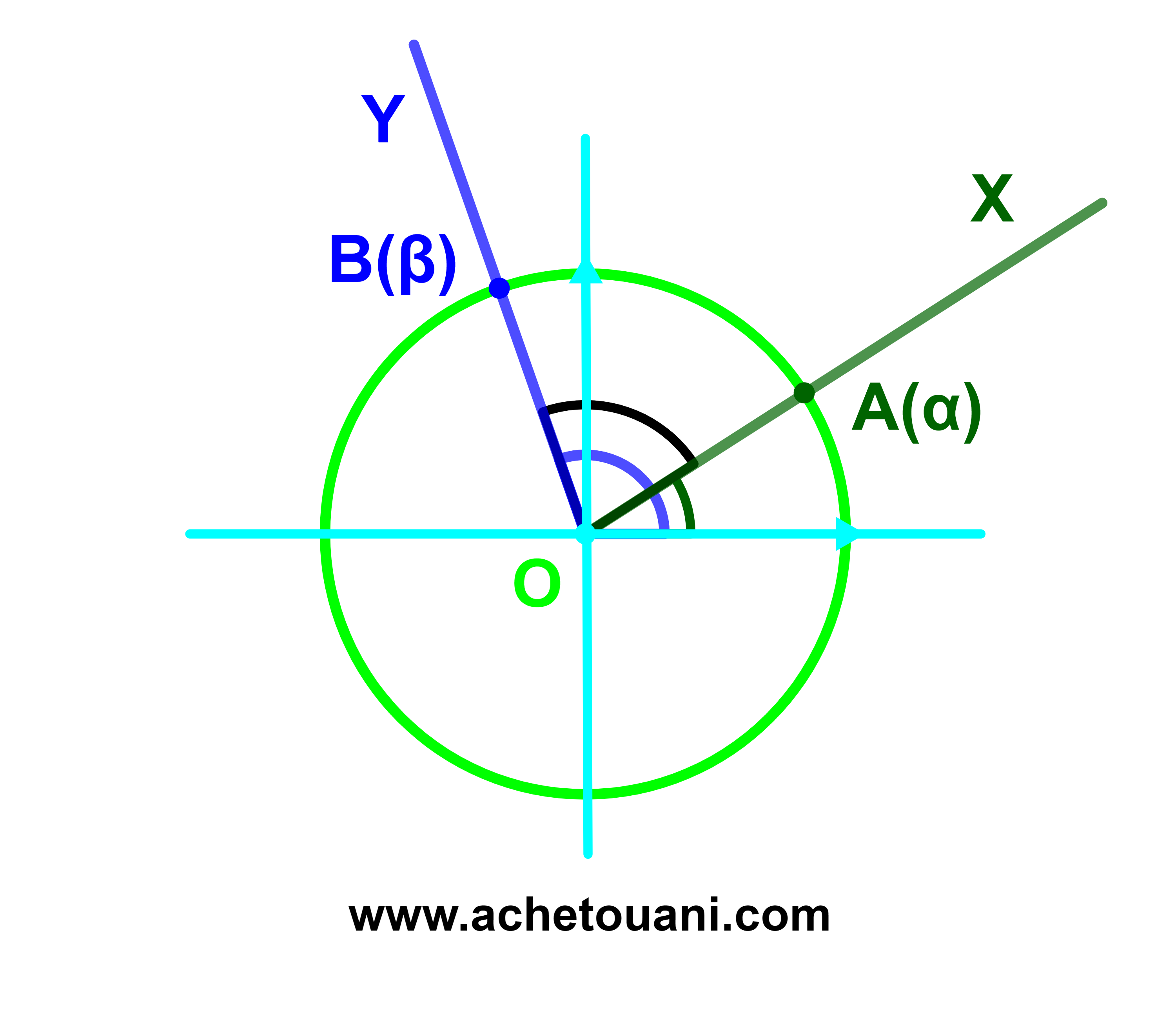
ليكن [OX) و [OY) نصفي ستقيم ويقطعان الدائرة المثلثية (C) على التوالي في A(α) و B(β).
الزاوية الموجهة لنصفي مستقيم [OX[ و [OY[ هي الزاوية الموجهة ([OA);[OB)).
([OX);[OY))= β-α+2kπ بحيث k∈ℤ.
3.1.2 تعريف
ليكن x قياسا منحنيا للزاوية الموجهة Ā.
نقول ان x هو القياس المنحني الرئيس للزاوية الموجهة Ā اذا كان x∈]-π;π].
مثال
لتكن A و B نقطتين من الدائرة المثلثية (C) بحيث.
| A( | 13π | ) et B( | 8π | ) |
| 3 | 4 |
حدد القياس المنحني الرئيسي للزاوية الموجهة ([OA);[OB)).
تصحيح
| ([OA);[OB))= | 8π | - | 13π | + 2kπ |
| 3 | 4 |
| -7π | ∈ ]-π ; π] |
| 12 |
| -7π | اذن |
| 12 |
هو القياس المنحنئ الرئيسي للزاةية الموجهة
([OA);[OB)).
3.1.3 علاقة شال
ليكن [OX) و [OY) نصفي مستقيم.
لكل نصف مستقيم [OZ)
([OX);[OY))≡
([OX);[OZ))+([OZ);[OY))[2π].