Exercice 1 tp

Montrer que les abscisses curvilines suivantes

x =	83π		y =	-117π		z =	123π
	4			4			4

représentent le même point M sur le cercle trigonométrique (C)

Correction

A savoir
x et y représentent un même point sur le cercle trigonométrique (C) signifie x≡y[2π].

En d'autre terme
x=y+2kπ tel que k∈ℤ signifie x et y ont la même abscisse principale.

x - y =	83π	-	-117π
	4		4

=	200π	=	2x25π
	4

donc x=y+2kπ avec k= 25∈ℤ ainsi x et y représentent le même point sur (C).

x - z =	83π	-	123π
	4		4
=	-40π	=	2x(-20)π
	4

x=z+2kπ avec k=-20∈ℤ ainsi x et z représentent le même point sur (C).
On a donc x≡y[2π] et x≡z[2π] alors y≡z[2π] et par conséquent x ; y et z représentent le même point sur (C).

Exercice 2 tp

Soit x l'abscisse curviligne principale du point M. Déterminer les abscisses curvilines du point M qui appartiennent à l'intervalle I dans chacun des cas suivants

x=	π		I=[	34π	;	43π	]
	4			3		3
x =	π		I=[	-33π	;	-13π	]
	5			5		5

Exercice 3 tp

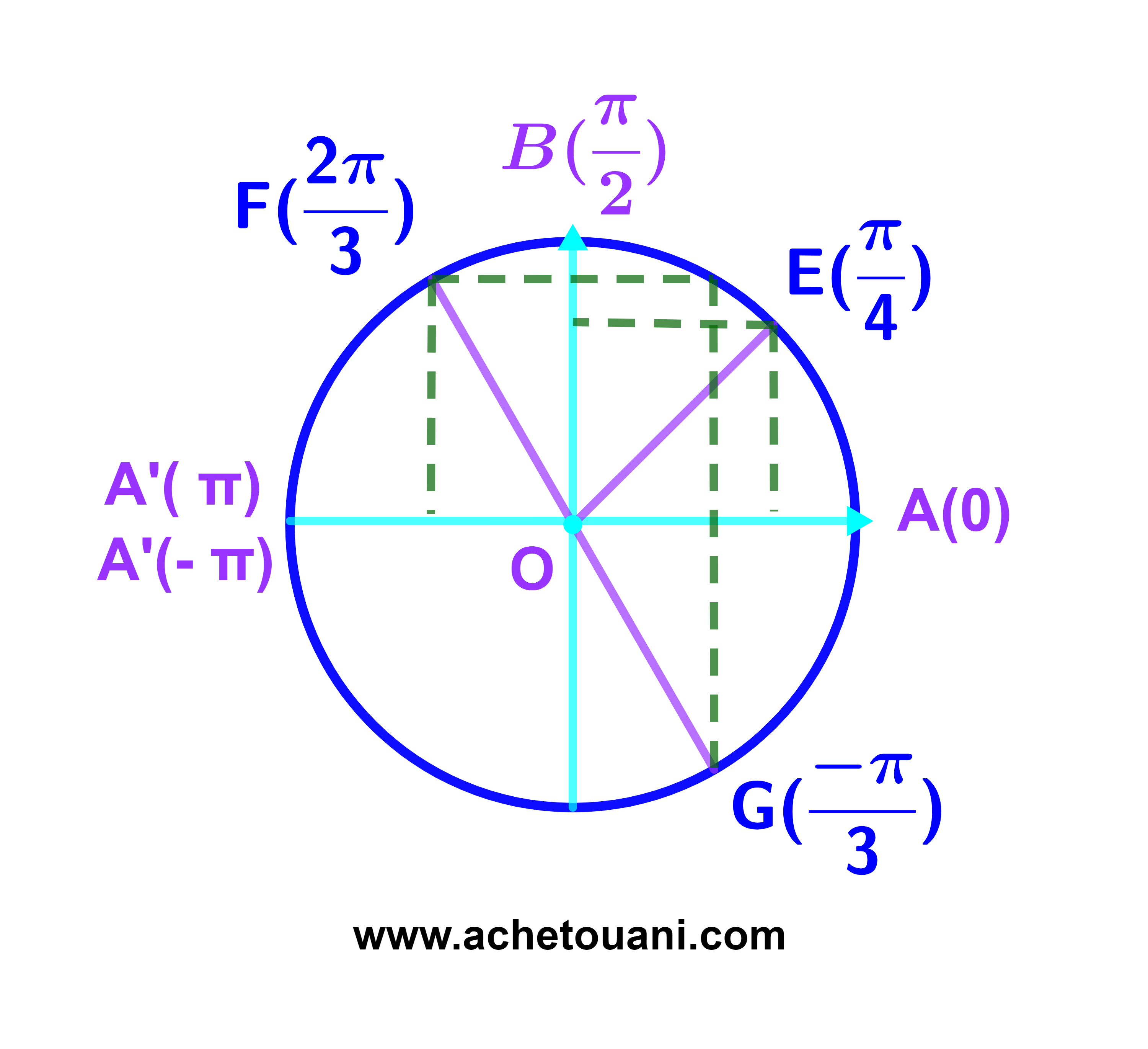
Déterminer l'abscisse principale des points

E(	41π	) ; F(	-28π	) ; G(	-13π	)
	4		3		3

et représenter les sur le cercle trigonométrique de cenre O.

Correction

1) L'abscisse principale du point E(a)
41÷4=10,25 et 10 est un nombre pair
donc 41π=4×10π+π.

a =	4×10π+π	=	π	+ 2×5π
	4		4

donc a =	π	∈]-π ; π]
	4

est l'abscisse principale du point E(a).
2) L'abscisse principale du point F(b).
28÷3=9,333.. et 9 est un nombre impair
28=3x8+4 mais 4>3
on prend le cas 28=3x10-2 car |-2|<3
donc -28π=3×(-10)π+2π.

b =	3×(-10)π+2π	=	2π	+ 2×(-5)π
	3		3

donc b =	2π	∈]-π ; π]
	3

est l'abscisse principale du point F(b).
3) L'abscisse principale du point G(c).

c =	3×(-4)π-π	=	-π	+ 2×(-2)π
	3		3

donc c =	-π	∈]-π ; π]
	3

c est donc l'abscisse principale du point G(c).