الحساب المثلثي (1_8)
3.2 الزاوية الموجهة لمتجهتين
3.2.1 خاصية وتعريف
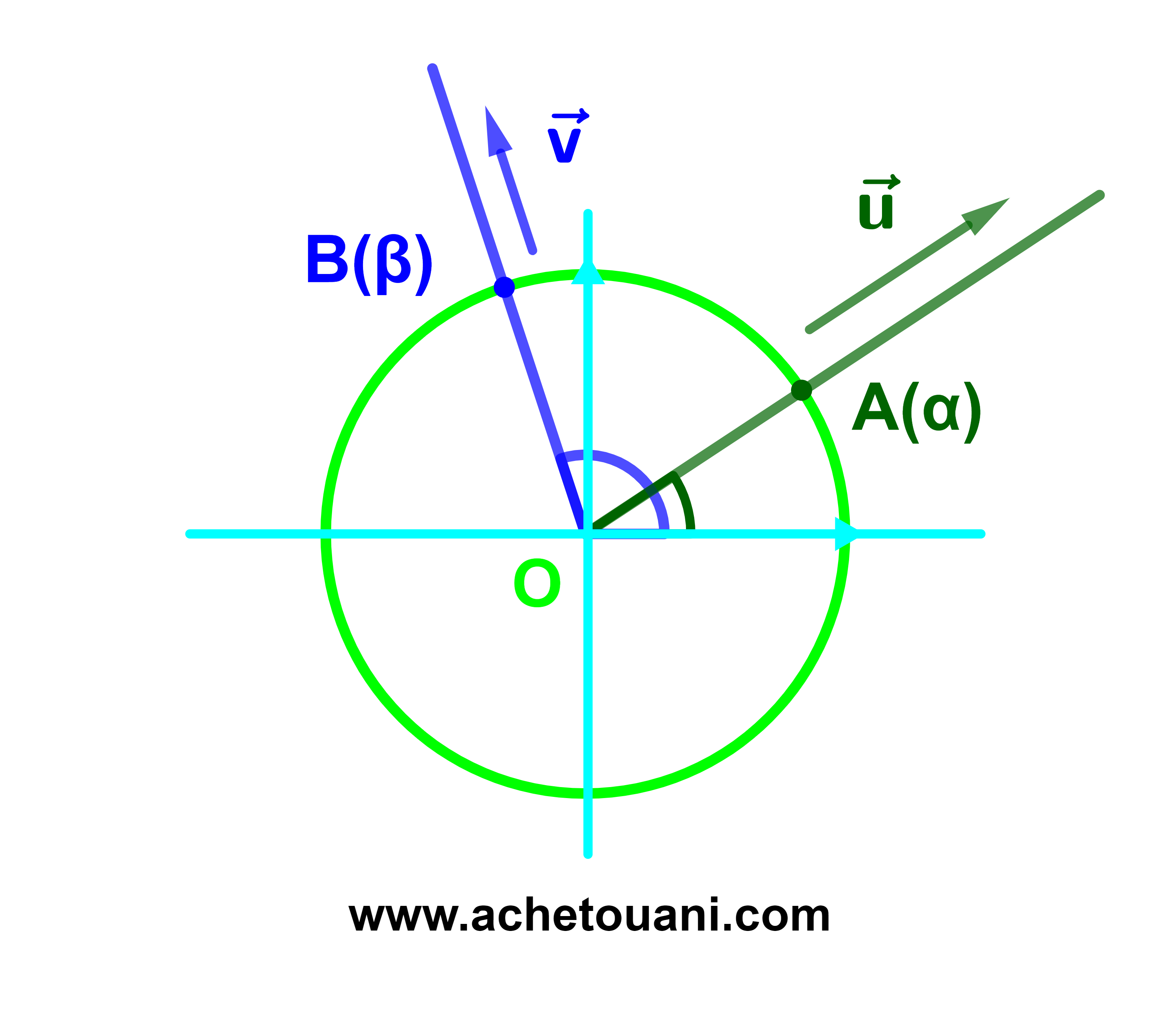
لتكن u→ و v→ متجهتين.
توجد نقطتين A و B في الدائرة المثلثية (C) بحيث
u→=tOA→
و v→= kOB→ و (t∈IR) و (k∈IR).
الزاوية الموجهة للمتجهتين u→ و v→
هي الزاوية الموجهة ([OA);[OB)).
لدينا اذن
(u;v)
=([OA);[OB))+2kπ بحيث k∈ℤ.
3.2.2 خاصيات
لتكن u→ و v→ و w→ ثلاث متجهات و k∈ℤ.
| (u ; v) = | - (v ; u) | |
| (u ; v) = | (u ; w) + (w ; v) + 2kπ | |
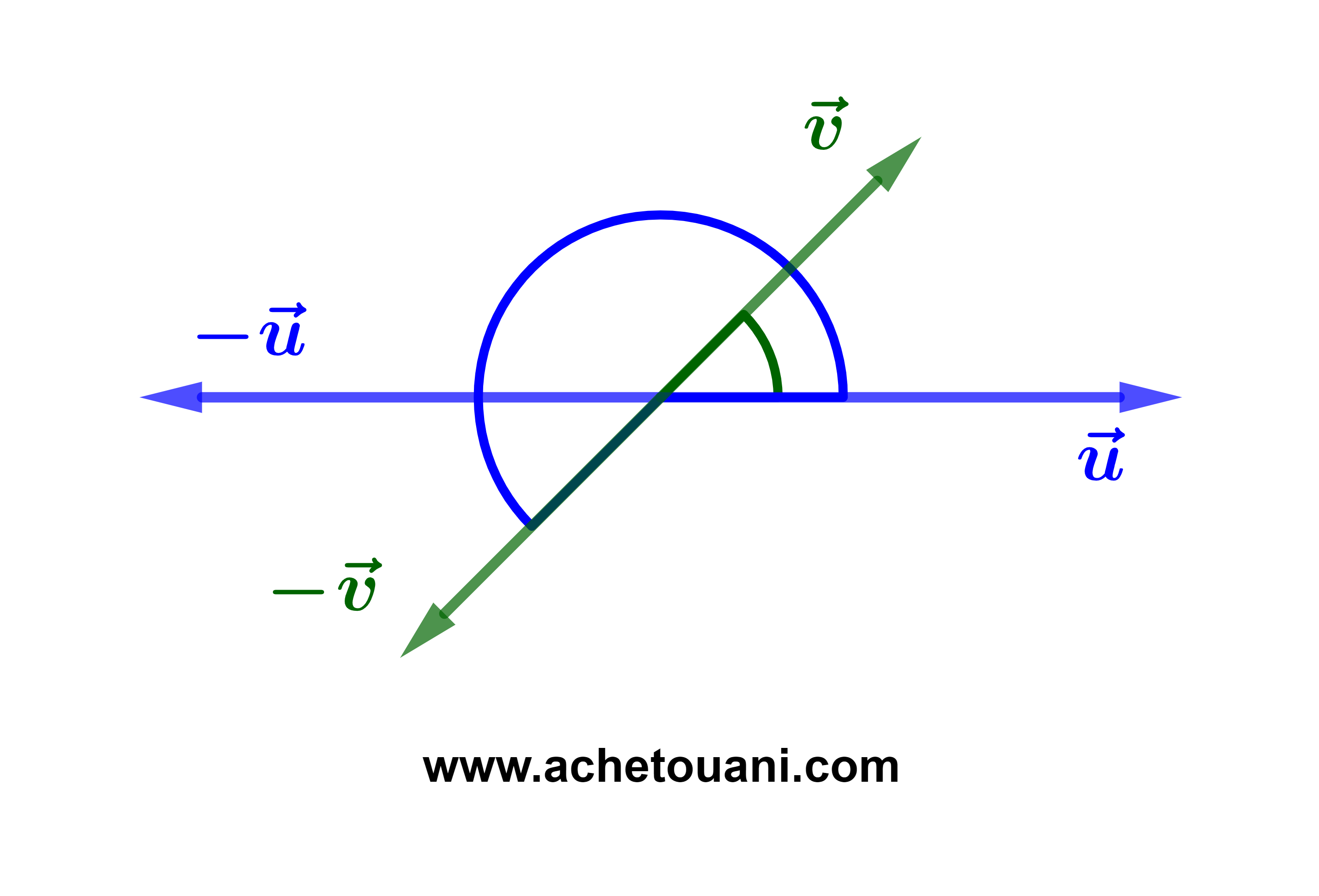
| (-u ; -v) = | (u ; v) + 2kπ | |
| (u ; -v) = | π + (u ; v) + 2kπ | |
| (- u ; v) = | π + (u ; v) + 2kπ | |
| (-u ; v) = | (u ; -v) |
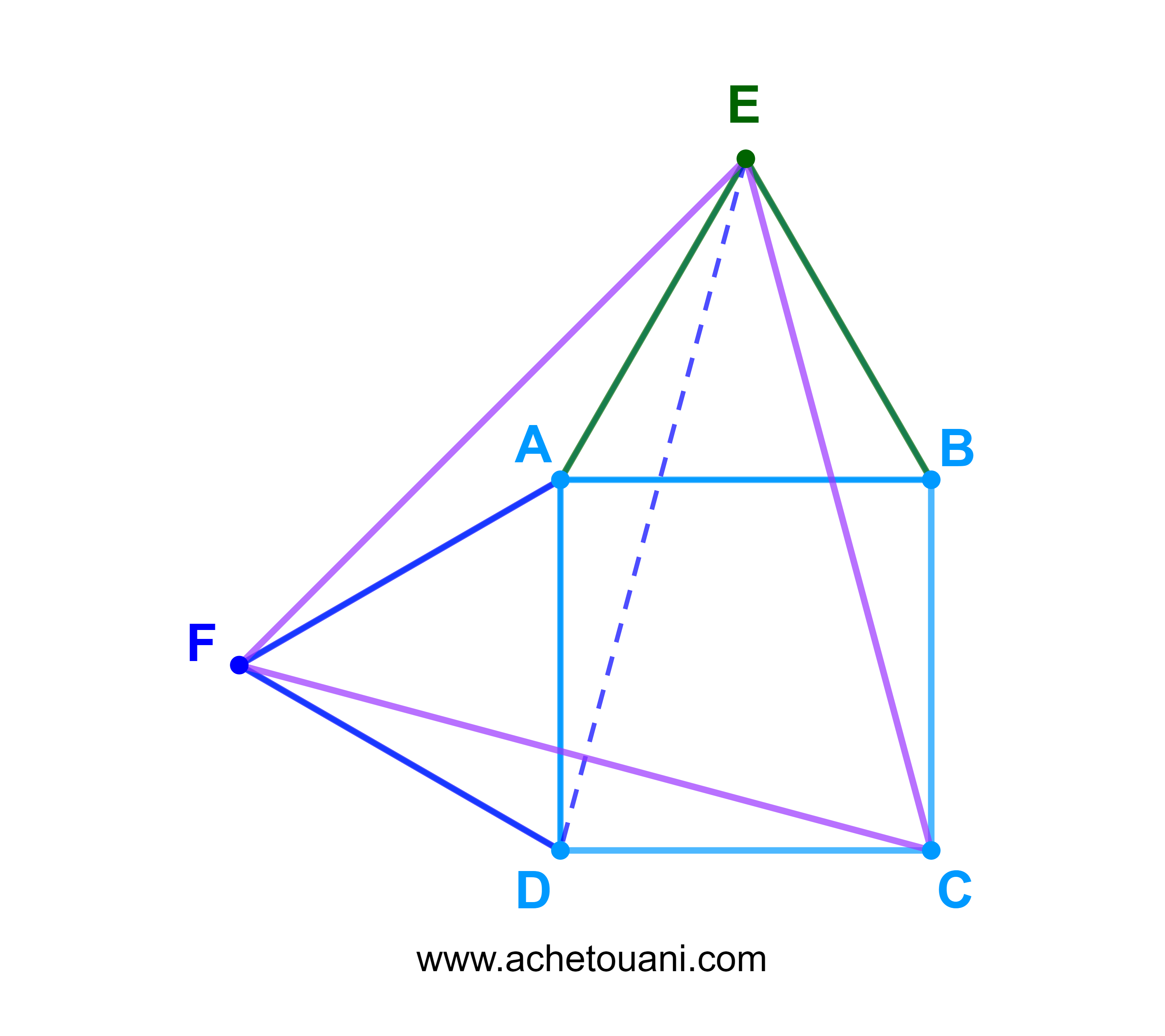
ترين 1 tp
ليكن ABCD مربعا. نعتبر نقطتين E و F بحيث EAB و FAD مثلثين متساويين الأضلاع.
1) حدد القياسات المنحنية لكل من الزاويات الموجهة (AE;AF) و (EC;EB).
2) استنتج طبيعة المثلث EFC.