تمرين 1 tp

احسب cosx و tanx بحيث

sinx =	-2	و x∈]	-π	;	π	]
	3		2		2

تصحيح

تذكير

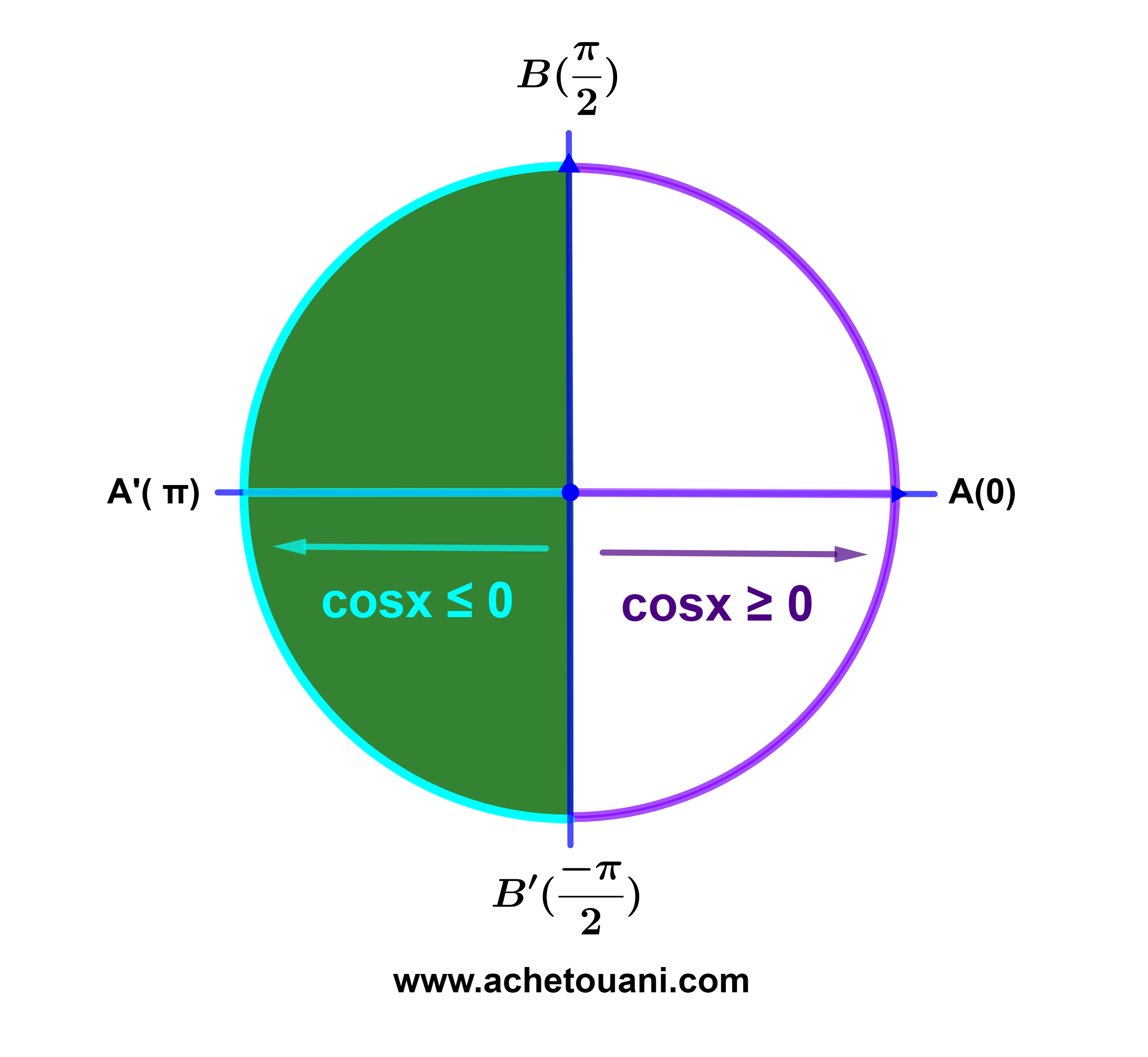
x∈[	-π	;	π	] → cosx≥0
	2		2

x∈[-π;	-π	] ∪ [	π	; π] → cosx≤0
	2		2

لدينا

x∈]	-π	;	π	]
	2		2

اذن cosx≥0
ومنه فان cosx=√(1-sin²x).

cosx = √(1-(	-2	)²) = √(	9-4	)
	3		9

cosx =	√(5)	اذن
	3

2) بما أن cosx≠0 فان tanx معرف.

tanx =	sinx
	cosx

وبالتالي

tanx =	-√(5)
	2

تمرين 2 tp

ليكن x∈]-π;0]

cos(x) =	2
	3

احسب tan(x) ثم sin(x).

تصحيح

cosx≠0 اذن tanx معرف.
نستعمل العلاقة

1+tan²(x) =	1
	cos²x

اذن

tan²(x) = -1 +	1	= -1+(	3	)²
	cos²x		2

تعني

tan²(x) =	-4+9	=	5
	4		4

نحدد اشارة tanx.
x∈]-π;0] اذن توجد حالتان

x∈]-π;	-π	[	(1
	2

اذن cosx≤0 وهذا غير ممكن لأن حسب المعطيات cosx>0.

x∈]	-π	;0]	(2
	2

اذن cosx≥0 ولدينا sinx≤0 اذن tanx≤0

tan(x) = -	√(5)	وبالتالي
	2

حساب sinx. لدينا sinx=cosx.tanx

sin(x) = -	√(5)	اذن
	3