تمرين 1 tp

نضع a=cos(13π-x)+cos(x+15π).

b = cos(	27π	+x)
	2

c = cos(	3π	-x)
	2

بسط a+b+c.

تذكير

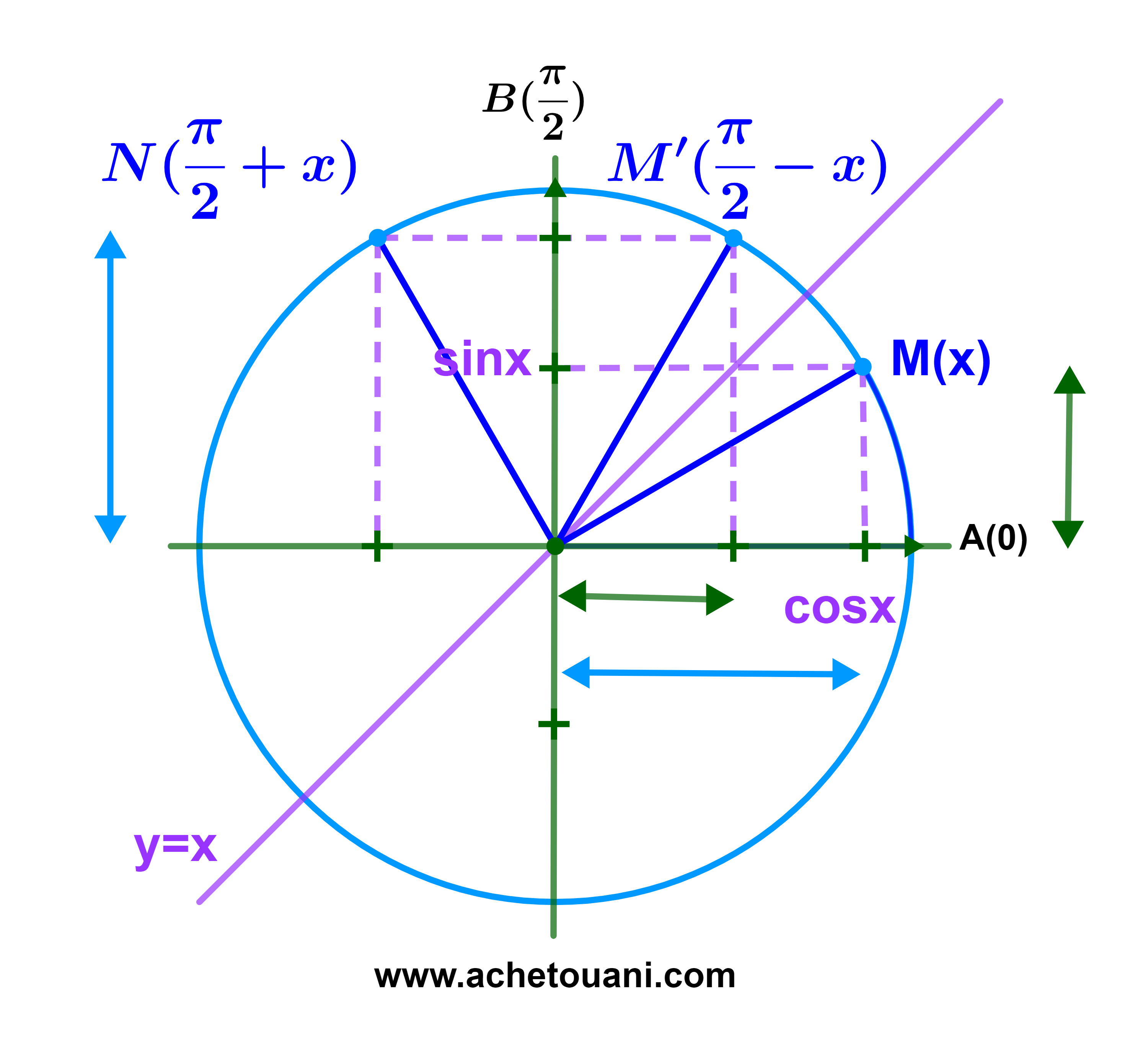
sin(	π	-x) = cosx
	2
cos(	π	-x) = sinx
	2
sin(	π	+x) = cosx
	2
cos(	π	+x) = - sinx
	2

تمرين 2 tp

نضع a=cos²(5π-x)+sin²(x+3π).

b = cos²(x-	7π	)
	2
et c= sin²(	-5π	-x)
	2

بسط a+b+c.

تمرين 3 tp

احسب sinx و tanx بحيث

cosx =	1	et x∈]-π;0]
	3

تصحيح

تذكير
اذا كان x∈[-π;0] فان sinx≤0.
اذا كان x∈[0;π] فان sinx≥0.

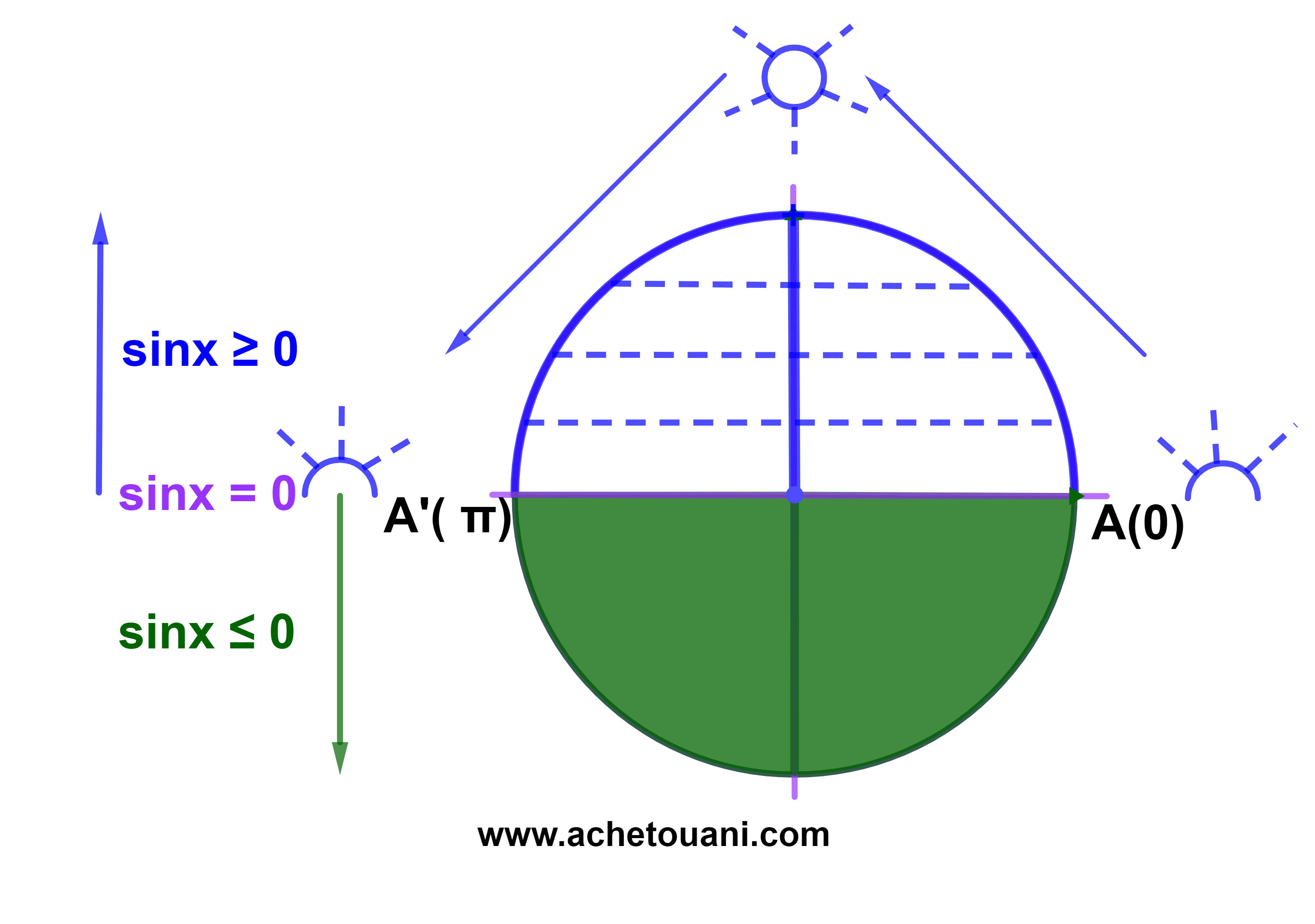
1) لدينا x∈]-π;0] اذن sinx≤0
اذن sinx=-√(1-cos²x).

sinx = - √(1-(	1	)²)
	3

= - √(	9-1	)
	9
=	- √(8)
	3

sinx =	- 2√(2)	اذن
	3

2) لدينا cosx≠0 اذن tanx معرق.

tanx =	sinx
	cosx

وبالتالي tanx=-2√(2).