تمرين 1 tp

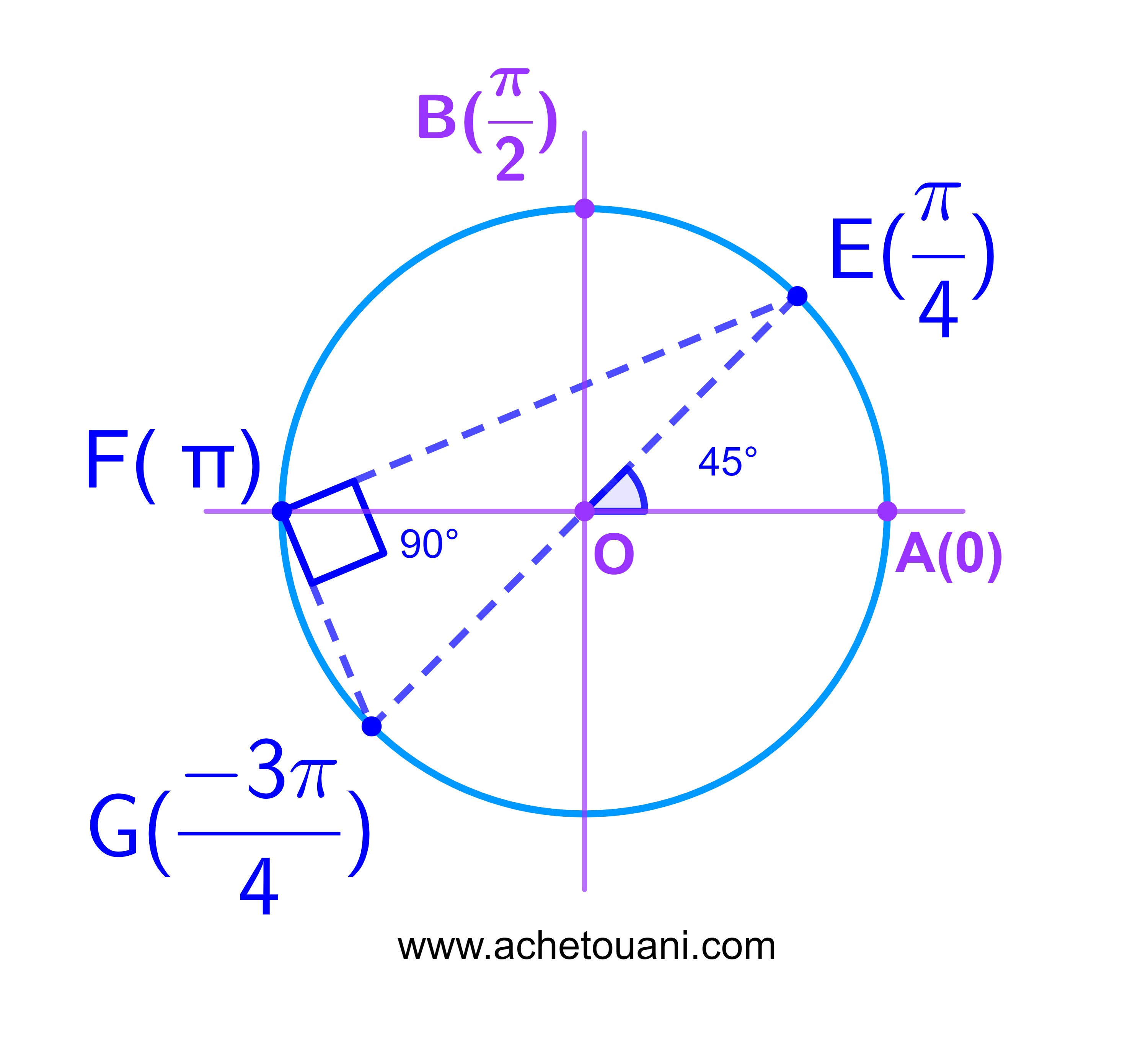
1) حدد الافصول الرئيسي لكل من النقط التالية

E(	201π	) و F(-13π)	و	G(	-3	)
	4				4

ومثلها على الدائرة المثلثية التي مركزها O
2) حدد القياس الرئيسي للزاوية الموجهة (OE;OG) واستنتج طبيعة المثلث EFG.

تصحيح

1) (q1) الافصول الرئيسي للنقطة E(a)
201÷4=50,25 اذن 201π=4×50π+π.

a =	4×50π+π	=	π	+ 2×25π
	4		4

ومنه فان

a =	π	∈]-π ; π]
	4

الافصول الرئيسي للنقطة E(a).

(q2) الافصول الرئيسي للنقطة F(b)
لدينا -13π=-14π+π=+π+2×(-7)π.
وبما ان π∈I فان الأفصول الرئيسي للنقطة F(b) هو π.
ملاحظة الكتابة -13π=-12π-π لا تقدم اجابة للسؤال
لان -π∉]-π;π].

2) القياس الرئيسي للزاوية الموجهة (OE;OG)
(OE;OG)≡b-c[2π]
اذن

(OE;OG) ≡	-3π	-	π
	4		4

ومنه فان

(FG;FE) ≡	-4π	=	-π[2π
	4

اذن [EG] قطر للدائرة المثلثية (C) وبالتالي المثلث EFG قائم في F.

تمرين 2 tp

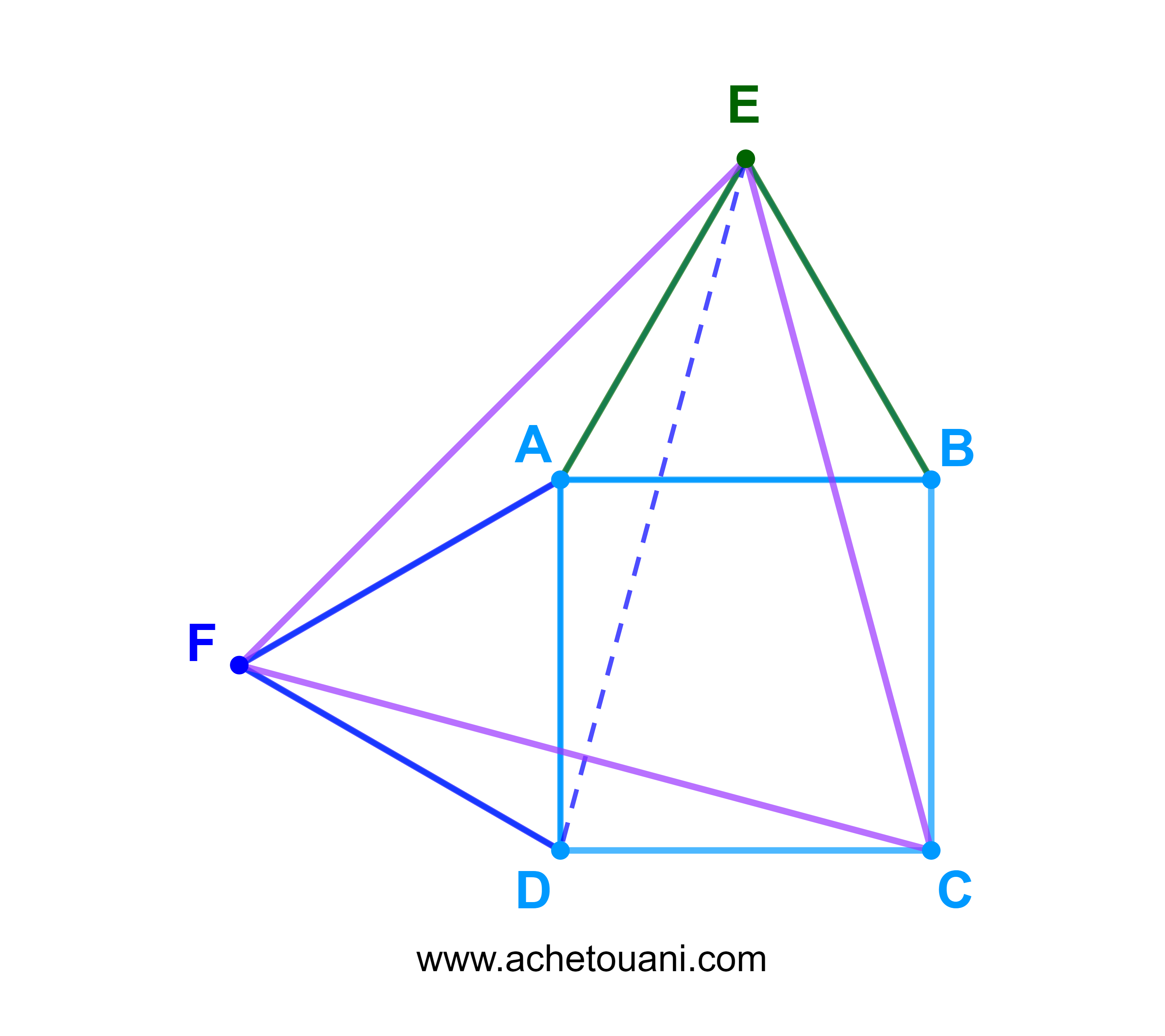
ليكن ABCD مربعا EAB و FAD مثلثين متساويي الاضلاع.
1) احسب القياس الرئيسي للزاوية الموجهة (AE;AF)
2) احسب القياس الرئيسي للزاوية الموجهة (EC;EB)
3) استنتج طبيعة المثلث EFC

تمرين 3 tp

ليكن ABCD مربعا و E نقطة داخل المربع و ABE مثلثا متساوي الأضلاع
النقطة H المسقط العمودي للنقطة E على المستقيم (CD).
1) حدد القياس الرئيسي لكل من الزوايا التالية
(AE;AD) و (DE;DA) و (DE;DH)
2) احسب EH واستنتج قيمة مقربة ل

cos(	-π	) و sin(	π	)
	12		12