Exercice 1 tp

1) Déterminer l'abscisse principale de

E(	201π	) et F(-13π)
	4

2) Déterminer la mesure principale de l'angle orienté (OE;OG) sachant que

G(	-3	)
	4

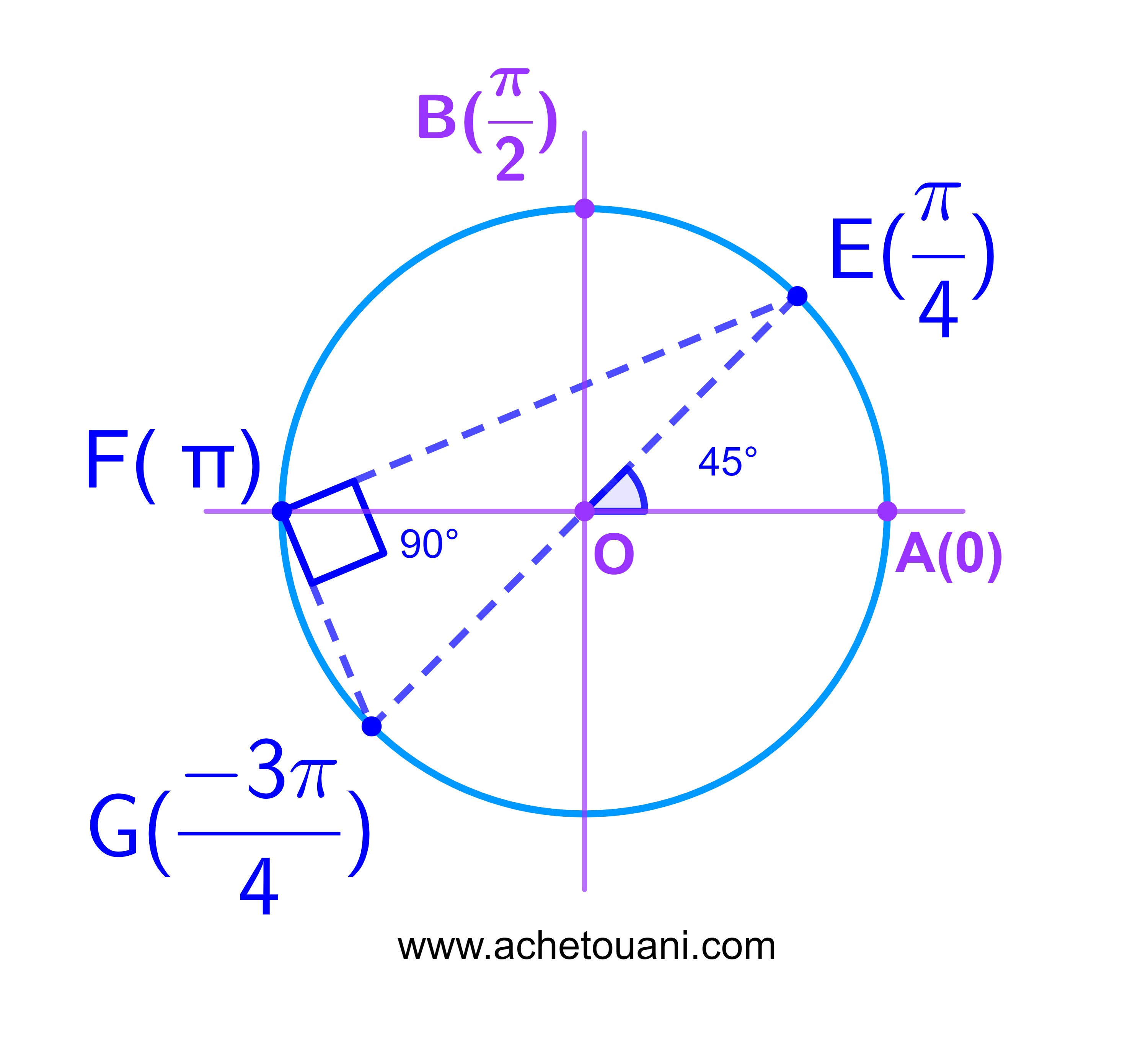
3) Représenter E ; F et G sur le cercle trigonométrique et déduire la nature du triangle EFG.

Correction

1) (q1) L'abscisse principale du point E(a)
201÷4=50,25 donc 201π=4×50π+π.

a =	4×50π+π	=	π	+ 2×25π
	4		4

ainsi a =	π	∈]-π ; π]
	4

est l'abscisse principale du point E(a).

(q2) L'abscisse principale du point F(b).
-13π=-14π+π=+π+ 2×(-7)π.
π∈I donc π est l'abscisse principale du point F(b).
Notons que si on écrit -13π=-12π-π alors ce cas nécessite un travail supplémentaire
car -π∉]-π;π].

2) Mesure principale de l'angle orienté (OE;OG).
(OE;OG)≡b-c[2π]

(OE;OG) ≡	-3π	-	π
	4		4

(FG;FE) ≡	-4π	=	-π[2π
	4

Donc [EG] est une diagonale de (C) ainsi EFG est un triangle rectangle en F.

Exercice 2 tp

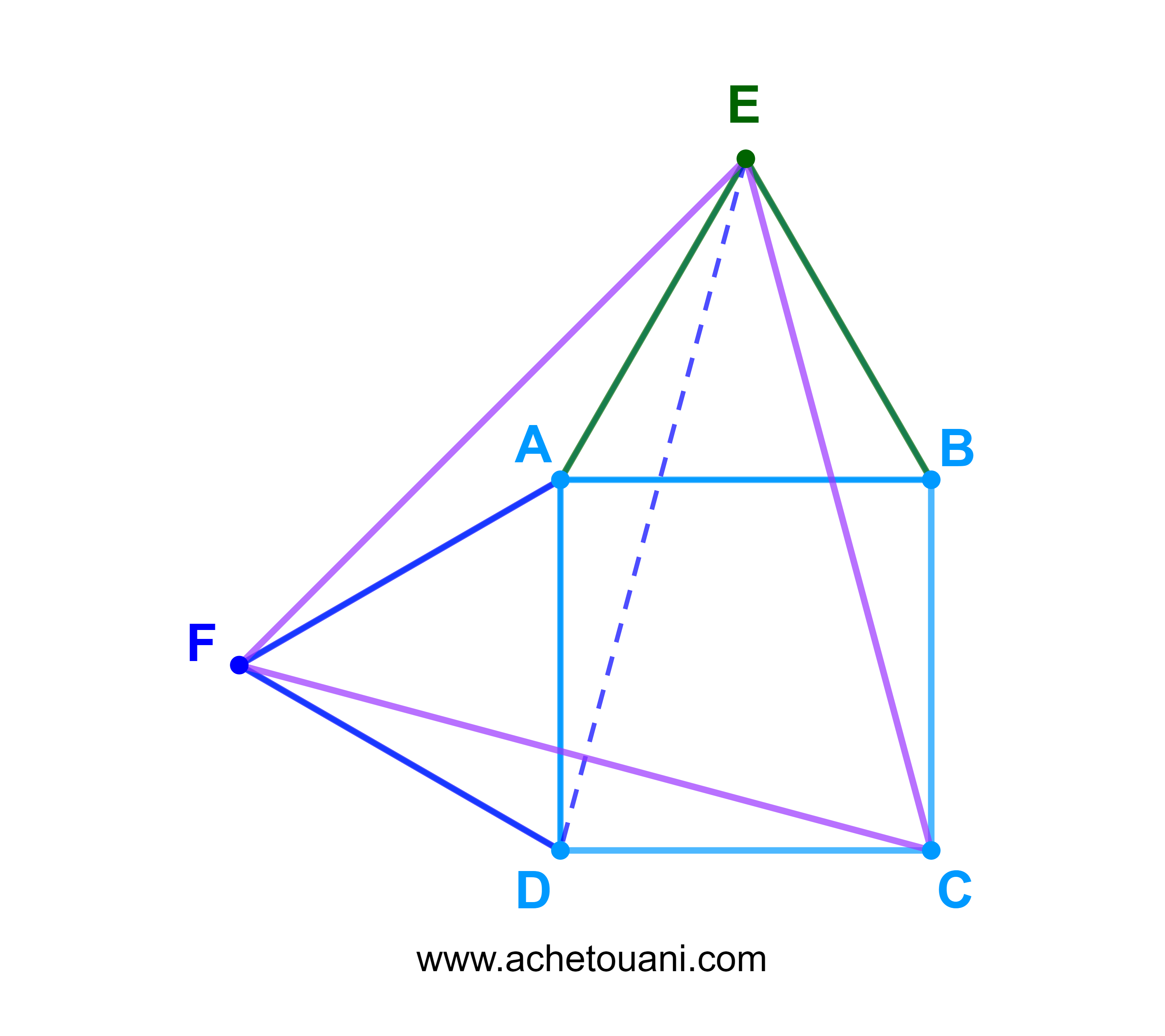
Soient ABCD un carré et EAB et FAD deux triangles équilatéraux.

1) Calculer la mesure de l'angle orienté (AE;AF)
2) Calculer la mesure de l'angle orienté (EC;EB)
3) Déduire la nature du triangle EFC

Exercice 3 tp

Soit ABCD un carré et E un point à l'intérieur du carré tel que ABE est un triangle équilatéral
le point H est le projeté ortogonal du point E sur la droite (CD).
1) Déterminer la mesure principale de chacun des angles orientés suivants
(AE;AD) ; (DE;DA) et (DE;DH)
2) Calculer EH et déduire une valeur approchée de

cos(	-π	) et sin(	π	)
	12		12