تمرين 1 tp

حل في IR المعادلة
(E): (√2)sinx-1=0.

تصحيح

(E): (√2)sinx-1=0 تكافئ

sinx =	√2
	2

لدينا

sin(	π	) =	√2
	4		2

اذن

أو	x =	π	+2kπ	(k∈ℤ و k'∈ℤ)
		4
	x = (π-	π	)+2k'π
		4

وبالتالي مجوعة حلول المعادلة (E)

S = {	π	+2kπ ;	3π	+2k'π }
	4		4

حيث (k∈ℤ و k'∈ℤ)

2.3 المعادلة cosx= a

2.3.1 حالات خاصة

1) اذا كان a=0 فان cosx=0 يعني

cosx = cos	π	= cos	- π
	2		2

يعني

أو	x =	π	+ 2kπ	(k∈ℤ و k'∈ℤ)
		2
	x =	- π	+ 2k'π
		2

يعني

k∈ℤ بحيث x =	π	+ kπ
	2

2) اذا كان a=1 فان cosx=1 يعني
cosx=cos0=cos(-0) يعني x=2kπ
اذن cosx=1 يعني x=2kπ بحيث k∈ℤ.
3) اذا كان a=-1 فان
cosx=cos-π=cosπ
اذن x=-π+2kπ أو x=π+2kπ.

لدينا π ≡ -π[2π]
اذن cosx=-1 يعني x=π+kπ.

2.3.2 خاصية

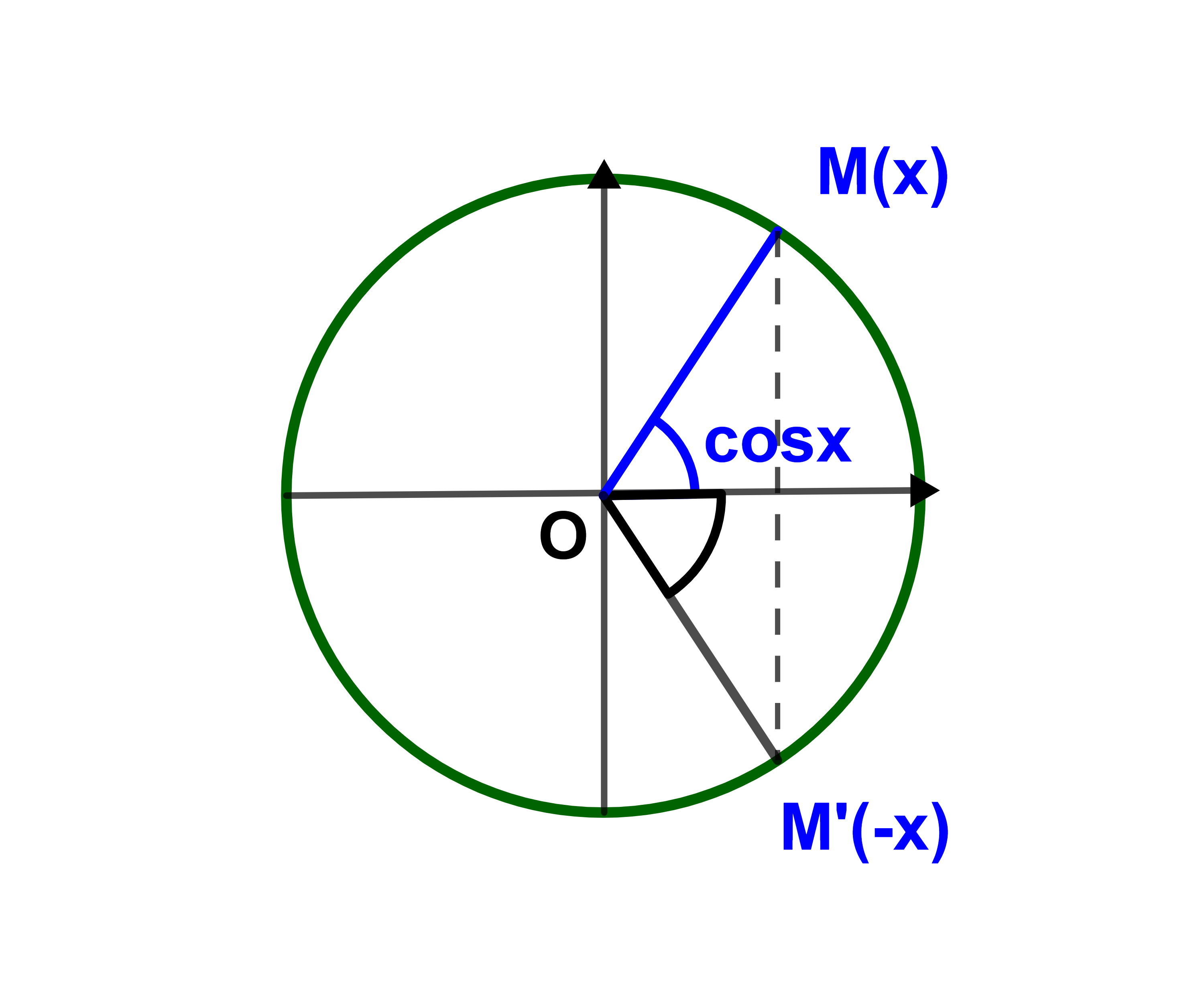
ليكن x∈IR و a∈IR. نعتبر المعادلة (E): cox=a و S مجموعة حلولها في IR.
1) اذا كان a>1 أو a<-1
فان المعادلة ليس لها حل.
2) اذا كان -1≤a≤1
قانه يوجد عدد حقيقي y بحيث cos(y)=a
بالاضافة الى ذلك
(x=y+2kπ) أو (x=-y+2kπ) بحيث k∈ℤ.
S={y+2kπ ; -y+2kπ/k∈ℤ و k'∈ℤ و cosy=a}.

تمرين 2

حل في IR المعادلة
(E): 2cosx-1 = 0.

تصحيح

(E): 2cosx-1=0 تكافئ

cosx =	1
	2

لدينا

cos(	π	) =	1
	3		2

اذن

أو	x =	π	+2kπ	(k∈ℤ و k'∈ℤ)
		3
	x = -	π	+2k'π
		3

وبالتالي مجموعة حلول المعادلة (E)

S = {	π	+2kπ ;	-π	+2k'π/ k∈ℤ و k'∈ℤ}
	3		3