3- المتراجحات المثلثية الأساسية

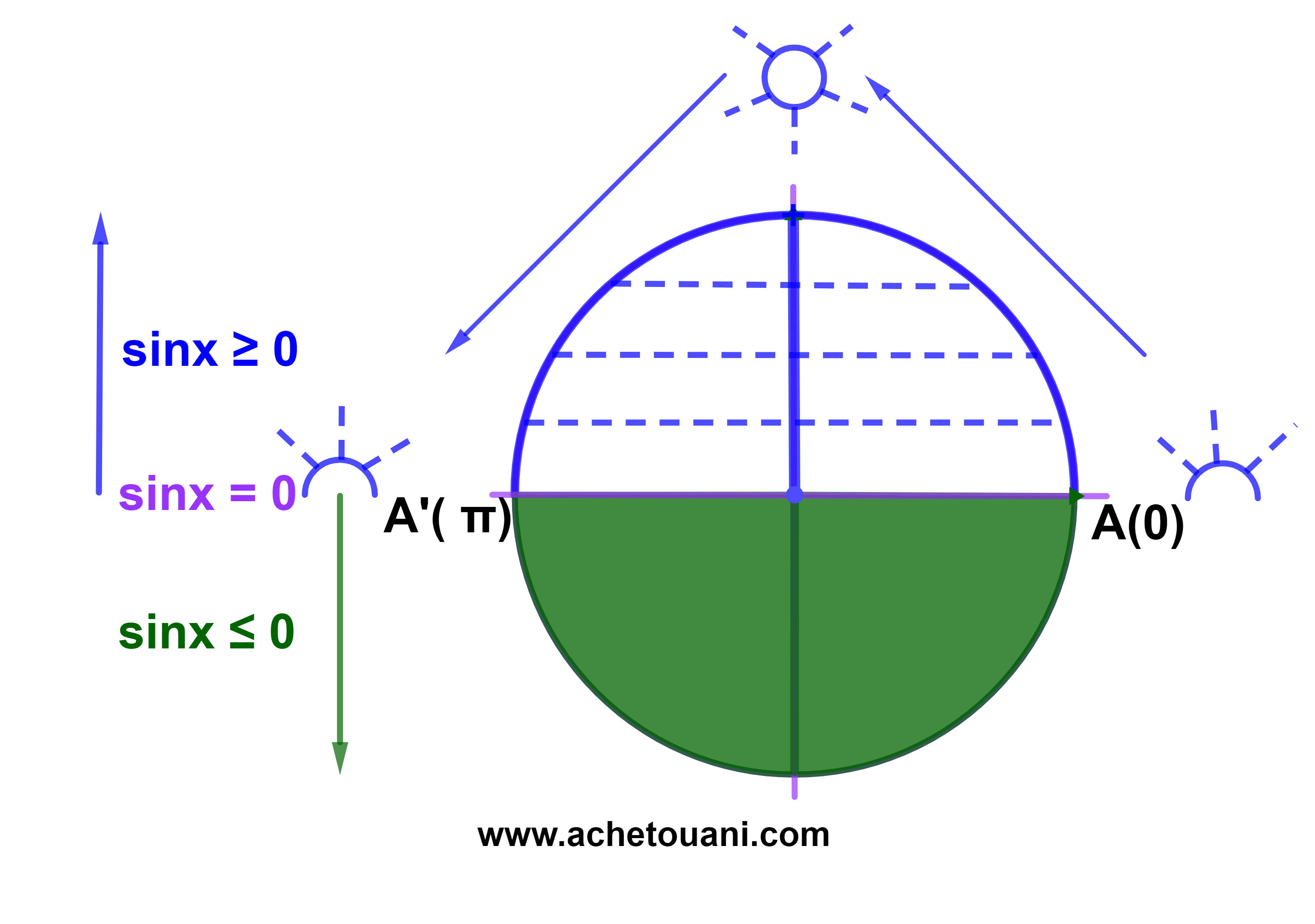
3.1 المتراجحة sinx≥a

3.1.1 خاصية

ليكن x∈IR.
اذا كان x∈[-π;0] فان sinx≤0.
اذا كان x∈[0;π] فان sinx≥0.

بصفة عامة
اذا كان x∈[-π+2kπ;0+2kπ] فان sinx≤0.
اذا كان x∈[0+2kπ;π+2kπ] فان sinx ≥0.

3.1.2 مثال

حل في I=[-π;π] المتراجحة
2sinx≥-√2.

تصحيح
2) نحل المعادلة
(E): 2sinx=-√2 في IR.
2sinx=-√2 تكافئ

sinx =	-√2
	2

sin(	-π	) =	-√2
	4		2

اذن (E) تكافئ

sinx = sin(	-π	)
	4

ومنه فان

k∈ℤ و k'∈ℤ حيث	x =	-π	+2kπ	أو
		4
	x = π -	-π	+2k'π
		4

2) نؤطر الحلول في المجال I=[-π;π].
(a) نأطير

-π ≤	-π	+2kπ	≤ π
	4

-1 ≤	-1	+ 2k	≤ 1
	4

يعني

-1 -	-1	≤ + 2k ≤ 1 -	-1
	4		4

يعني

-3	≤ k ≤	5
8		8

k∈ℤ اذن k=0 ومنه فان

x =	- π
	4

(b) نأطير

-π ≤	5π	+ 2k'π	≤ π
	4

يعني

-1 ≤	5	+ 2k'	≤ 1
	4

يعني

-1 -	5	≤ + 2k' ≤ 1 -	5
	4		4

يعني

-9	≤k'≤	-1
8		8

k'∈ℤ اذن k'=-1 ومنه فان

x =	- 3π
	4

3) نثل هذه الحلول على محور أو على الدائرة المثلثية (C)
(-π)---(-3π4)---(-π/2)---(-π/4)---(0)
(0)---(π/2)---(π)
وبالتالي

S = [-π	;	-3π	]∪[	-π	;	π]
		4		4